

Precedente Indice generale Home Indice moduli Successiva
6_ Frequenza delle correnti rotoriche
Le correnti indotte sul rotore sono dovute alla velocità di taglio relativa N del campo rotante rispetto al rotore. Pertanto la loro frequenza, ricordando le relazioni (2), (3) e (1) vale
![]()
7_ F.E.M. statoriche e rotoriche
Il motore è confrontato con il trasformatore, individuando nello statore il primario e nel rotore il secondario. Esiste quindi nello studio quest’analogia, che servirà come riferimento e collegamento con la teoria del trasformatore.
In particolare si richiama il fatto che, mentre nel trasformatore il campo magnetico varia con direzione fissa e ampiezza variabile, nel motore le variazioni sono dovute alla direzione continuamente variabile, mentre l’ampiezza del campo è costante. Si ritiene, infatti, per semplicità, che il campo si distribuisca con andamento sinusoidale nel traferro: il fenomeno di induzione elettromagnetica avviene con le stesse conseguenze rispetto ai due avvolgimenti primario e statorico, avvolgimento secondario e rotorico.
Le variazioni del flusso che interessano gli avvolgimenti di statore e di rotore inducono delle f.e.m. che, in analogia ai risultati ottenuti con il trasformatore, sono espresse da relazioni in cui si evidenziano proporzionalità col flusso, con il numero di spire e con la frequenza.
A questo proposito, mentre la frequenza della tensione impressa allo statore è quella di rete f1, si osserva che per il rotore la frequenza f2 = f1.s è legata allo scorrimento (v. rel. 5). Quindi anche le grandezze rotoriche, dipendenti dalla frequenza, sono funzione dello scorrimento, e di ciò si terrà conto, scrivendo ad esempio E2(s), Z2(s), I2(s).
Per la f.e.m.i. in una fase dello statore dalla variazione del flusso prodotto dal campo magnetico rotante si ha
in cui
·
E1 = valore efficace della f.e.m. indotta in una fase statorica;·
K1 = coefficiente di Kapp, che dipende dalla collocazione dei conduttori dell’avvolgimento nelle cave e dal fattore di forma (si veda la giustificazione fatta per la macchina sincrona);·
f1 = frequenza della tensione di alimentazione;·
Φ = valore efficace del flusso utile che si concatena con gli avvolgimenti di statore e di rotore;·
N1 = numero delle spire in una fase dell’avvolgimento.
In modo analogo per la f.e.m.i. in una fase del rotore, tenendo conto però che il numero delle cave di rotore è diverso da quello di statore (ad esempio per evitare o ridurre impuntamenti) e che quindi è diverso il fattore di Kapp, e ricordando ancora che la frequenza di rotore è f2 = f1.s, si ha
E2(s) = K2.f2.Φ.N2 = K2 . f1 . s . Φ . N2 (2)
Osservando che la (2), nel caso in cui si sostituisca s con 1 per ricavare la f.e.m. indotta all’avviamento, ovvero con rotore fermo (appunto con s = 1) si ha la relazione
![]()
per cui la (2) si può anche scrivere più concisamente
![]()
8_ Schemi di statore e rotore
Rispettando l’analogia con il trasformatore e adottando pertanto la stessa simbologia, si può attribuire al motore asincrono il seguente schema elettrico completo.

Figura 1) Primo schema elettrico di una fase del motore asincrono
La simbologia adottata e il significato dei componenti sono quelli del trasformatore:
Ø
R1 e X1 = resistenza di una fase dell’avvolgimento e reattanza di dispersione statorica;Ø
Ra = tiene conto delle perdite nel ferro di statore;Ø
Xμ = giustifica la corrente di magnetizzazione necessaria a produrre il flusso dell’accoppiamento mutuo;Ø
I1(s) = corrente totale assorbita da una fase dello statore;Ø
Io = corrente assorbita a vuoto;Ø
I’1(s) = corrente di reazione statorica necessaria a controbilanciare la f.m.m. secondaria e tale che K1 N1 I’1(s) = - K2 N2 I2(s) ;Ø
E1 = f.e.m.i. di statore;Ø
E2(s) = f.e.m.i. di rotore, variabile in funzione dello scorrimento s;Ø
I2(s) = corrente in una fase dell’avvolgimento rotorico;Ø
X2(s) = reattanza dei flussi dispersi, funzione dello scorrimento;Ø
R2 = resistenza di una fase dell’avvolgimento rotorico.
Osservando che, come è stato svolto per E2(s), si può analogamente scrivere
![]()
E’ possibile ora calcolare la corrente rotorica con le seguenti espressioni:
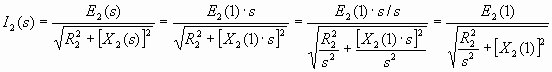
Dall’ultima uguaglianza si può concludere che per produrre la corrente I2(s) è necessario un generatore che eroghi una f.e.m. costante E2(1) e che l’ostacolo al passaggio della corrente è un’impedenza formata da una resistenza variabile R2/s e da una reattanza che non è più variabile, bensì fissa, con valore costante X2(1).
Questa specie di artificio matematico consente di sostituire al primo schema elettrico rotorico di fig.1) questo secondo di figura 2), certamente equivalente al primo, in cui l’unica grandezza variabile è R2/s .
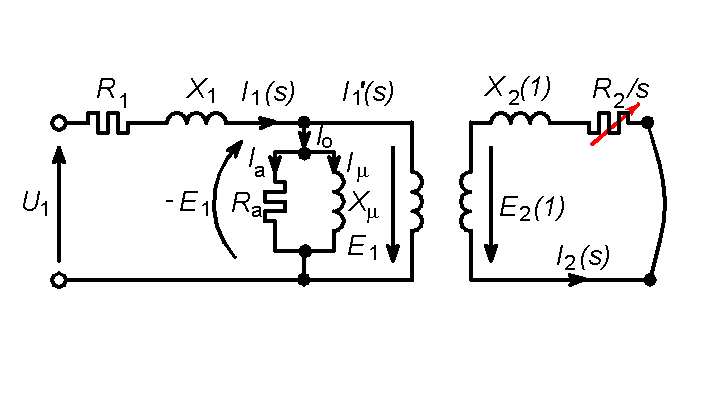
Figura 2) Secondo schema del motore in cui E2(1) e X2(1) non sono più variabili, ma varia R2/s
Lo schema precedente, con un piccolo banale artificio, può diventare praticamente simile a quello di un trasformatore: alla R2/s si sottrae R2 (e si ottiene una resistenza di carico Ru); basta ora aggiungere la resistenza appena tolta R2 in serie alla X2(1) e si ottiene il terzo schema di fig. 3).

Figura 3) Terzo schema del motore asincrono, perfettamente equivalente a quello di un trasformatore
Stando così le cose, si possono ripetere, con le necessarie precauzioni, gran parte delle considerazioni colà svolte e che saranno rispolverate all’occorrenza.
Qui il carico del motore può solo essere considerato di tipo resistivo, siccome in Ru(s) variabile
![]()
va la potenza meccanica che viene trasferita quasi tutta sull’albero e utilizzata nelle varie condizioni di carico richieste al motore. Naturalmente per ogni condizione di carico cambia la velocità di rotazione del rotore: quasi uguale a quella di sincronismo nel funzionamento a vuoto, minore quanto maggiore sarà la richiesta di carico, per cui Ru, come la corrente I2(s), dipenderanno dalla velocità e quindi dallo scorrimento s . Stessa sorte toccherà alla corrente assorbita dallo statore, funzione anch’essa del carico applicato all’albero.
La fig. 3) chiarisce le analogie più volte citate fra asincrono e trasformatore:
Ø
con s = 0 si ha Ru = ∞ e lo schema corrisponde al funzionamento a vuoto (circuito di rotore aperto);Ø
con s = 1 si ha Ru = 0 e lo schema è quello del funzionamento in C.°C.°
I diagrammi vettoriali tensione-corrente di statore e rotore si ricavano come nel trasformatore.
|
Ω1 - Ω2 rispetto al rotore, che a sua volta gira con velocità Ω2 rispetto a un osservatore fisso con lo statore. Quindi la corrente di rotore e la sua f.m.m. ruotano, sempre rispetto al riferimento fisso statorico, alla velocità Ω1 - Ω2) + Ω2 = Ω1 e pertanto la reazione d’indotto tra le f.m.m. rotorica e statorica si possono sommare alla frequenza sempre costante, in modo da ripristinare le condizioni magnetiche del funzionamento a vuoto. I vettori delle f.m.m. sono quindi in sincronismo con il flusso per qualunque velocità rotorica, e quindi per qualsiasi scorrimento. Si possono quindi associare le grandezze ai vettori.La stessa reazione avviene dunque come nel trasformatore (macchina notoriamente a flusso costante). Qui però le c.d.t. dei parametri serie di statore non sono trascurabili, come non lo è la corrente assorbita a vuoto, per cui l’asincrono, a differenza del trasformatore, non lavora proprio a flusso costante al variare del carico (si ricorda che il flusso è proporzionale alla E1, che differisce dalla U1 per le c.d.t. citate). Tuttavia i risultati che si ottengono con questa semplificazione, che sarà adottata ancora in seguito, sono accettabili per le applicazioni. |