

Precedente Indice generale Home Indice moduli Successiva
11_ Variazione delle correnti al variare dello scorrimento
Con riferimento allo schema di fig. 2 _8_ qui sotto riportato, si esaminano i comportamenti delle correnti della macchina al variare dello scorrimento, cominciando dalla corrente rotorica I2(s), per poi passare successivamente alla corrente di reazione I’1(s) e alla corrente totale I1(s) assorbita dallo statore.

Figura 1) Schema del rotore e dello statore, di cui si trascureranno le c.d.t. dovute a R1 e a X1.
Si esaminano in tabella, in forma schematica, i campi di funzionamento della macchina, per i valori di scorrimento significativi, al variare di n2 = (+ ∞) ÷ (- ∞), deducibili dalla relazione
![]()
|
n 2 |
s |
I 2(s) |
Funzionamento |
|
∞ |
-∞ |
|
Velocità infinita del rotore nello stesso senso del campo rotante. Punto comune a s = ∞ |
|
(∞)÷(>n1) |
(-∞)÷(<0) |
I2 < 0 (generata) |
GENERATORE |
|
n2 = n1 |
s = 0 |
I2 = 0 (rotore aperto) |
Vuoto ideale |
|
n1> n2 ≥0 |
0< s ≤ 1 |
|
MOTORE |
|
n2 =0 |
s = 1 |
|
Avviamento del MOTORE (corto circuito) |
|
n2 < 0 |
s > 1 |
|
Si inverte il senso di rotazione del rotore rispetto a quello del campo rotante. FRENO |
|
n2 = - ∞ |
s = ∞ |
|
Punto comune a s = -∞ Senso di rotazione opposto a quello del campo induttore. |
Per giustificare il comportamento della corrente rotorica al variare dello scorrimento occorre esaminarne le seguenti espressioni.
Partendo dalla relazione ottenuta nel precedente §8, moltiplicando numeratore e denominatore per X2(1) e osservando che, con scorrimento infinito, la stessa espressione diventa
![]()
(corrente a 90° in ritardo rispetto alla E2(1), poiché R2/s=0) e si ottengono le relazioni
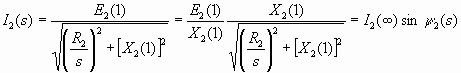
in cui sinψ2 è relativo al triangolo dell’impedenza rotorica che si sta esaminando (fig.2).
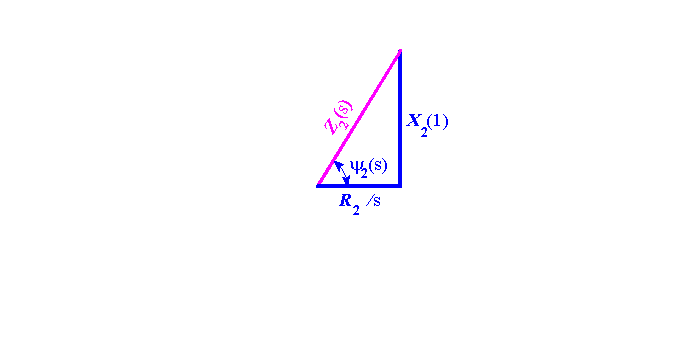
Figura 2) Triangolo dell’impedenza di rotore
Da questa relazione conclusiva
![]()
si deduce che, al variare dello scorrimento, la corrente generica I2(s) è un cateto di un triangolo rettangolo, dovendo essere di 90° l’angolo formato tra la I2(s) e l’altro cateto che la congiunge alla I2(∞), con ψ2(s) lo sfasamento tra la f.e.m. rotorica E2(1) e la corrente rotorica in esame (v. fig. 3).
La corrente I2(∞) è l’ipotenusa del triangolo. L’angolo di 90° degli infiniti triangoli (al variare di s) insiste sulla circonferenza il cui diametro è la stessa I2(∞). Pertanto, qualunque sia il valore dello scorrimento, l’estremo del vettore I2, come ad esempio il punto P" della corrente rotorica, scorre sulla circonferenza di rotore della fig. 3.
Tra i valori particolari si cita la corrente rotorica I2(1) allo spunto del motore (s=1), mentre nella condizione di vuoto ideale (s=0) la corrente rotorica è nulla, essendo il circuito rotorico aperto (origine del diagramma cartesiano).
In stretta analogia con il trasformatore e trascurando la c.d.t. complessivamente prodotta dalla resistenza di fase R1 dell’avvolgimento di statore e dalla reattanza X1 dei flussi dispersi, si può impostare il fenomeno della reazione d’indotto.
Infatti, la presenza della corrente rotorica, con il campo rotante da essa generato, tende a modificare il flusso di statore. Trascurando però le c.d.t. ora citate e osservando lo schema della fig. 1, si conclude che la E1 coincide in modulo con la tensione U1 e poiché la tensione di alimentazione è costante, sarà costante il flusso generato dalla E1, per qualsiasi condizione di carico. A controbilanciare il disturbo introdotto dal campo rotante creato dalla corrente rotorica, lo statore assorbirà dunque dalla rete la corrente di reazione I’1(s) tale da soddisfare la relazione
K1 N1 I’1(s) = - K2 N2 I2(s)
come avviene nel trasformatore, contrastando la f.m.m. rotorica con un’onda opposta di f.m.m. rotante statorica. Come conseguenza, il flusso risultante rimane costante, come deve essere.
Per ottenere la corrente totale I1(s) assorbita dallo statore si somma alla corrente di reazione I’1(s) la corrente costante del funzionamento a vuoto Io. Ciò è rappresentato in fig.3, in corrispondenza della generica corrente rotorica I2(s). L’estremo della risultante I1(s) è il punto P’.
Se per maggior semplicità grafica si ritiene che sia K1 N1 = K2 N2, nel calcolare le correnti di statore la corrente di reazione I’1(s) avrà lo stesso modulo della corrispondente I2(s). Naturalmente, in generale, il modulo della corrente di reazione può essere minore o maggiore rispetto alla I2, in base al rapporto di trasformazione della macchina, e di conseguenza anche i diametri delle due circonferenze saranno legati dallo stesso rapporto.
Anche le correnti di reazione avranno il loro estremo sul cerchio il cui diametro sarà coincidente, secondo l’ipotesi fatta, con quello di rotore, cioè
![]()
(Si sottolinea che questa uguaglianza esiste solamente se K1 N1 = K2 N2 e quindi, ritornando all’analogia col trasformatore, è come se il rapporto spire fosse unitario).
Il cerchio delle correnti di reazione viene dunque traslato con l’origine sull’estremità della corrente costante Io e le correnti di statore avranno anch’esse il loro estremo sul cerchio del primario (diagramma circolare primario o diagramma di Heyland), molto importante per le applicazioni e per varie giustificazioni sul comportamento e sul funzionamento della macchina asincrona in generale. Sarà ancora oggetto di studio successivamente, come diagramma di Heyland.
In seguito si esaminerà anche, con maggiori dettagli, la condizione di funzionamento relativa alla macchina "generatore", nel semicerchio rotorico superiore e nel semicerchio statorico inferiore. Nel funzionamento da motore e da freno ci si riferisce al semicerchio inferiore di rotore e al diagramma circolare statorico, posto sopra l’asse delle ascisse.
La figura 3 riporta il diagramma circolare delle correnti rotoriche al variare dello scorrimento, in tutto il campo di funzionamento della macchina asincrona e, di conseguenza, il corrispondente comportamento delle correnti di statore, di cui il cerchio di destra è il luogo dei loro estremi.
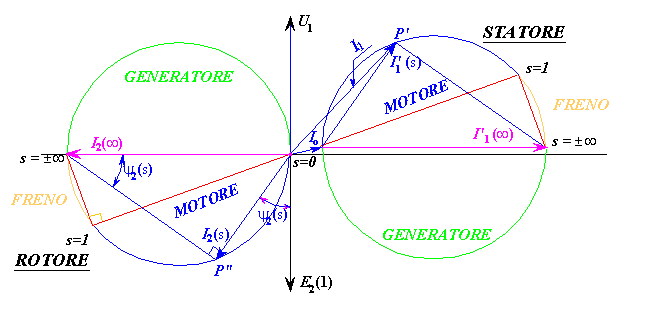
Figura 3) Diagramma circolare delle correnti rotoriche e statoriche, in tutto il campo di funzionamento della macchina asincrona (
motore, freno, generatore).