

Precedente Indice generale Home Indice moduli Successiva
14_ Il diagramma circolare di Heyland
Il diagramma circolare consente di valutare, per ogni punto di funzionamento della macchina, tutte le caratteristiche, come ad esempio la corrente assorbita, lo sfasamento, la coppia, la potenza assorbita, ecc.
Nel §11_ si è verificato che, al variare dello scorrimento, e quindi della velocità di rotazione del rotore rispetto al campo magnetico rotante, sia le correnti di rotore, sia quelle di statore ad esse legate, hanno il loro estremo che insiste su una circonferenza, il cui diametro è la corrente che corrisponde allo scorrimento infinito (s=∞).

Figura 1) Digramma delle correnti, nel funzionamento completo della macchina asincrona, tracciato in base al 1° schema della fig. 2.
Per riferirci al diagramma delle correnti di statore e, in particolare, al funzionamento della macchina come motore, si consideri lo schema equivalente, con i parametri rotorici riportati allo statore (si ricorda che per portare un’impedenza dal rotore allo statore occorre moltiplicarla per n2, essendo per definizione n = E1/E2(1) ), secondo quanto risulta dalla fig.2.

Figura 2) Lo schema del motore con rotore separato dallo statore e, in basso, lo schema equivalente semplificato, riportato a statore.
Si ricorda che la resistenza rotorica R2/s, riportata a statore, tiene conto della resistenza complessiva rotorica, cioè carico + resistenza di fase del rotore (vi si impegna tutta la potenza sincrona).
La Xe’ è invece la somma della X1 e della X2(1) riportata allo statore e valgono le seguenti espressioni
Nello schema equivalente semplificato della macchina, con riporto delle grandezze rotoriche allo statore, si è spostato il ramo trasversale a monte della R1 e X1: pertanto la macchina viene considerata funzionante a flusso costante, qualunque sia il carico del motore.
Questa semplificazione operativa porta a una peggiore approssimazione rispetto a quanto accade per il trasformatore, a causa della presenza non trascurabile, qui, della corrente a vuoto Io. Tuttavia, per le applicazioni, quest’ipotesi semplificativa non altera sostanzialmente le conclusioni che si desidera raggiungere. In particolare, se lo scorrimento è basso, gli errori si riducono.
Dallo schema in basso di fig. 2 si può inoltre dedurre che
, per la condizione di s=∞, si ha la seguente situazione
per cui la corrente di reazione non si va a collocare a 90° in ritardo rispetto alla U1 (come accadeva lavorando con lo schema di statore, separato da quello di rotore della fig. 2 in alto). Il ritardo è deducibile dall’angolo
ψ(∞) ed è inferiore a 90°, tanto più quanto maggiore è la resistenza dell’avvolgimento di statore R1. Naturalmente con s=∞ è nulla la resistenza complessiva che proviene dal rotore.La corrente di reazione statorica a cui corrisponde lo scorrimento s=∞ si colloca quindi più in alto sul cerchio, rispetto al diagramma circolare ricavato in precedenza per la fig. 1
(come si può vedere dal diagramma di fig. 3, il punto s=±∞ si è spostato dalla posizione S discussa in precedenza, al punto H).
15_ Costruzione del diagramma di Heyland
Per costruire il diagramma circolare delle correnti statoriche occorre ricordare che il cerchio si può individuare sapendo che, in particolare, la corrente a vuoto Io e quella di spunto Icc insistono su una circonferenza. Per il tracciamento occorre conoscere, come già si è detto:
·
la misura della resistenza di fase R1T dell’avvolgimento di statore (riportata alla temperatura convenzionale di 75°C);·
la corrente assorbita Io e il relativo sfasamento φo dedotti dalla prova a vuoto;·
la corrente statorica di avviamento Icc e il relativo sfasamento φcc riportati alla temperatura convenzionale, dedotti dalla prova in corto circuito.·
Si stabilisce la scala delle correnti, ad esempio
|
|
Seguendo ora la costruzione secondo la simbologia della fig. 3, intendendo rappresentare per il momento sull’asse delle ordinate la tensione di fase del motore, si collocano in scala, e con gli sfasamenti ricavati, sia la corrente Io, a cui corrisponde s≈0, sia la corrente all’avviamento Icc, per la quale è s=1.
Ø
Si congiungono i loro estremi che, si sa, apparterranno al cerchio e quindi il segmento PoPcc sarà una corda del cerchio da costruire.Ø
L’asse della corda PoPcc, che occorre tracciare in figura, passa per il centro del cerchio; il centro del cerchio sta nel mezzo del diametro; il diametro che consideriamo è quello che parte dall’estremo della Io ed è orizzontale, parallelo cioè all’asse delle ascisse. Per individuarlo come diametro si fa partire dal punto Po una semiretta orizzontale che, nel punto di intersezione con l’asse della corda PoPcc, individua finalmente il centro C.Ø
Col compasso si centra C, con apertura pari al raggio PoC e si costruisce finalmente il cerchio, che sicuramente passerà anche per Pcc.
Come si utilizza il cerchio
Ø
Il cerchio è il luogo geometrico degli estremi di tutte le correnti di statore e se ne disegna una qualsiasi, che parte dall’origine degli assi e arriva nel generico punto P. Da P si abbassa la verticale fino al punto A, posto sull’ascissa. Il segmento PA vale![]()
e quindi è la componente attiva della corrente in esame.
Tuttavia, considerando la radice quadrata di 3 e la tensione di alimentazione, il segmento può rappresentare, in opportuna scala, la potenza assorbita quando il motore assorbe la corrente I1.
La scala delle potenze assorbite, ricordando quella scelta per le correnti, diventa
|
|
Ø
L’asse delle ascisse diventa la linea di riferimento delle potenze assorbite: a partire dall’estremo di una corrente statorica, abbassando la verticale, si troverebbe la componente attiva della corrente, che però nella scala delle potenze reali diventa la potenza assorbita dal motore.In particolare, potendosi ritenere costanti le perdite meccaniche e nel ferro per qualunque corrente di carico, la semiretta uscente da Po e parallela a quella delle potenze assorbite, delimita il tratto in cui le perdite a vuoto saranno sempre ritenute costanti.
Si riprenderà in seguito qualche chiarimento in merito.
Ø
La potenza assorbita massima si ha tracciando la parallela all’asse delle potenze assorbite, tangente al cerchio e misurando la distanza rispetto al "livello zero delle potenze assorbite" (è la verticale che passa per il centro del cerchio e vale Pa Max in fig. 3).Ø
La retta delle potenze rese all’albero (la potenza meccanica utile) si può individuare trovando due punti di funzionamento per i quali la potenza resa sia nulla:- un punto è Po, perché a vuoto il motore non trascina alcun carico;
- un altro punto è Pcc, poiché con il rotore bloccato non si fornisce potenza utile.
La retta passante per Po e Pcc è quindi la retta di riferimento delle potenze rese.
Partendo da una corrente di carico qualsiasi (ad esempio la corrente I1), si misura la lunghezza del segmento PB e la si moltiplica per la scala delle potenze, ottenendo così la potenza sull’albero, per la condizione di lavora scelta.
Ø
La potenza resa massima si ha individuando la tangente al cerchio, parallela alla retta di riferimento delle potenze rese (segmento Pr Max).Ø
Poiché per il segmento PQ valgono le espressioni analoghe a quelle ricavate per il riferimento della potenza assorbita dal motore![]()
si conclude che l’asse delle ordinate può essere considerato il riferimento della potenza reattiva, scambiata fra la rete di alimentazione e il motore. La scala ha la stessa misura ricavata per le potenze reali, ma ovviamente l’unità di misura è il var.
Ø
Per il riferimento della potenza sincrona occorre individuare il segmento PccE, dalla verticale passante per il punto a scorrimento unitario. Dal punto F si riporta, con la scala delle potenze, la perdita nel rame di statore prodotta dalla Icc e data dalla relazione![]()
a cui corrisponde, in watt, il segmento FG.
|
Ø
Definita la retta di riferimento delle potenze sincrone, considerata la proporzionalità fra potenza e coppia sincrona, in base alla relazione![]()
si può considerare la stessa retta come riferimento per la coppia sincrona, cambiando semplicemente la scala.
|
|
Con questa scala si determinano, in particolare:
·
la coppia prodotta nella condizione di funzionamento in P, data dal segmento verticale PK;·
la coppia all’avviamento o coppia di spunto PccG;·
la coppia massima, ottenuta tracciando la tangente al cerchio, parallela alla retta di riferimento delle coppie (segmento TMax). La zona di funzionamento stabile è compresa fra Po e il punto di coppia massima; il tratto instabile fra il punto di coppia massima e Pcc.
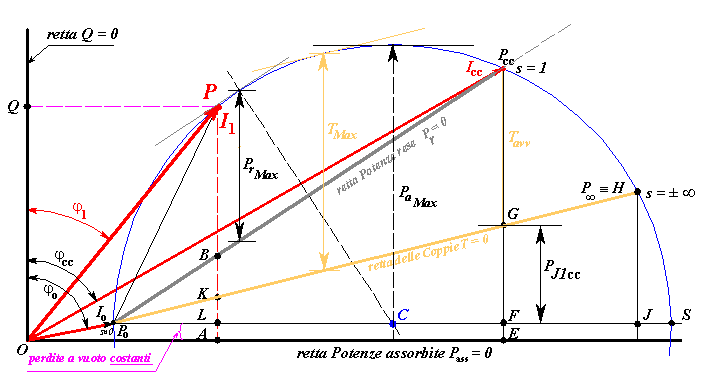
Figura 3) Costruzione del diagramma circolare delle correnti statoriche.
16_Determinazione dello scorrimento e del rendimento
Dal diagramma di fig. 3, per la condizione di carico che corrisponde al punto P, si deducono, nelle rispettive scale:
·
corrente assorbita I1 = PO nella scala delle correnti·
corrente a vuoto Io = PoO nella scala delle correnti·
corrente di reazione I’1 = PPo nella scala delle correnti·
fattore di potenza del motore in quella condizione di carico = cosφ1·
potenza attiva assorbita = PA nella scala delle potenze·
potenza reattiva = PQ·
potenza resa = PB·
potenza sincrona = PK·
perdita nel rame di statore = KL·
perdita nel rame di rotore = BK·
perdite meccaniche e perdite nel ferro = LA·
coppia generata = PK (nella scala delle coppie)·
scorrimento =BK/PK, essendo s=Pcu2/Ps (sul diagramma questo rapporto è di difficile lettura, viste le dimensioni dei segmenti)·
rendimento = PB/PA = Presa/Passorbita (anch’esso di difficile determinazione per l’esiguità dei segmenti)
Per rendere più precisa la determinazione dello scorrimento e del rendimento si utilizzano costruzioni grafiche particolari, che consistono in un’amplificazione di scale sfruttando dei triangoli simili.
Per ricavare lo scorrimento occorre (fig. 4):
a) tracciare la tangente alla circonferenza in Po (con la costruzione corretta del diagramma, la tangente non sarà verticale);
b) prolungare la retta delle potenze rese;
c) individuare, parallelamente alla retta delle coppie, un segmento divisibile in 100 parti, compreso tra la tangente e il prolungamento della retta delle potenze rese.
d) Per conoscere lo scorrimento che corrisponde alla condizione di carico individuata ad esempio dal punto P, si prolunga la corrente di reazione che parte da Po e va a tagliare in s1 la retta di riferimento degli scorrimenti. Se la scala va da 0 a 1 si legge lo scorrimento; se è divisa da 0 a 100 si legge lo scorrimento percentuale.
Si osservi che i triangoli individuati dai punti 1-0-Po e P-K-Po sono simili, come pure s1-0-Po e B-K-Po. La costruzione ha amplificato la lettura delle grandezze Pcu2 = BK e Ps1 = PK.
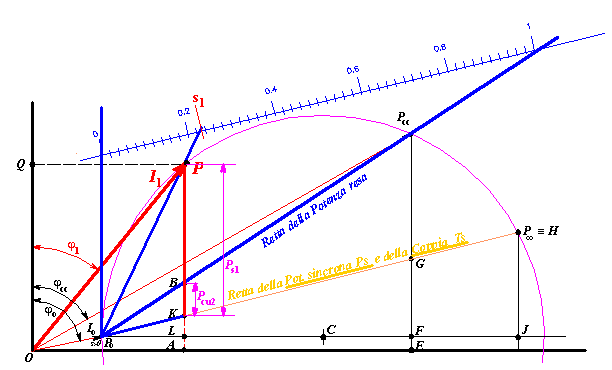
Figura 4) Determinazione dello scorrimento per il punto di funzionamento
P
Per ricavare il rendimento occorre (fig. 5):
a) Si prolunga la retta di riferimento delle potenze rese PoPcc fino ad incontrare l’ascissa nel punto W e si prosegue fino ad R0.
b) Da W si traccia la parallela alla tangente al cerchio in Po (con il cerchio avente il centro corretto la tangente in Po non è verticale come qui).
c) Fra queste due direzioni si traccia un segmento orizzontale che sarà diviso in 100 parti uguali (scala che va da 0 a 1, o da 0 a 100 per il η%).
d) Il rendimento relativo al generico punto P si ottiene partendo dall’estremo della corrente in gioco e passando per il punto W fino a tagliare la retta del rendimento, dove se ne legge il valore direttamente.
La giustificazione del procedimento grafico è simile a quella relativa al calcolo dello scorrimento. Il rendimento relativo al funzionamento nel punto P si ottiene dal rapporto fra potenza resa PB e la potenza assorbita PA. Poiché i segmenti sono di dimensioni ridotte, anche qui si ricorre ad un’amplificazione grafica delle scale, sfruttando la similitudine fra triangoli, facilmente individuabili dal grafico di fig. 5.
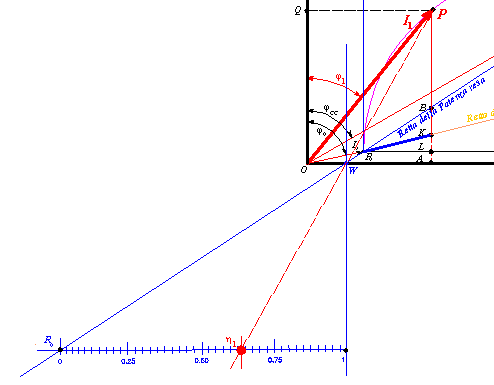
Figura 5) Scala amplificata del rendimento.