Indice generale Home Indice moduli
Correnti
alternate – Sistemi MONOFASE
![]()
Si considerano, in questa parte, i circuiti con parametri ideali, utile premessa alla successiva rappresentazione che terrà conto della effettiva costituzione circuitale.
Si analizzano i comportamenti in regime sinusoidale di una resistenza pura, di un’induttanza pura e di una capacità pura.
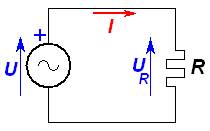
Figura 1) Resistenza pura alimentata da una sorgente in c.a. : valori efficaci, coincidenti, della tensione applicata U e della caduta di tensione UR ai capi della resistenza.
Se si applica agli estremi di una resistenza R (fig.2) la d.d.p. sinusoidale di equazione
![]()
la corrente che percorre la resistenza seguirà le vicende della tensione, risultando quindi in fase con essa e con ampiezza calcolata in ogni istante dalla legge di Ohm, ovvero dal rapporto fra il valore della tensione e della resistenza in esame:
![]()
Passando ai valori efficaci della tensione e della corrente si scrive
![]()
Alle grandezze sinusoidali si associano i vettori i quali, per quanto è già stato detto, generalmente hanno come modulo il valore efficace (e non il valore massimo), che viene indicato con la lettera maiuscola.

Figura
2) Diagrammi vettoriale e temporale
della tensione applicata e della corrente che percorre una resistenza pura.
Applicando ai capi della bobina pura (priva di resistenza e con induttanza costante) una tensione sinusoidale, anche la corrente che l’attraversa è sinusoidale, ma le loro condizioni di fase e le loro ampiezze sono di tipo particolare.
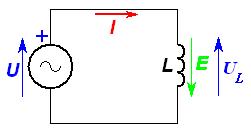
Figura 3) Circuito puramente induttivo
Si parta dal presupposto che la corrente che attraversa la bobina sia sinusoidale, con equazione temporale
![]()
Si vuole determinare la tensione da applicare ai capi della bobina in modo che vi circoli la corrente (1).
Una corrente variabile crea un flusso variabile, legati dalla relazione
![]()
La variazione del flusso concatenato fa nascere, per la legge dell’induzione elettromagnetica, una f.e.m. indotta
(v. unità 3 http://www.barrascarpetta.org/m_0_s0/m0s0u3.htm)
che ostacola le variazioni della corrente:
![]()
Dalla trigonometria, essendo
![]()
la (3) si può scrivere
![]()
Associando la f.e.m.i. (4) ad un vettore (fig.4), questo si troverà in ritardo rispetto al vettore corrente, associato a sua volta alla corrente espressa dalla (1).
Nel circuito elementare formato dal generatore che produce una tensione sinusoidale u(t) e dalla bobina pura ai cui capi è presente la f.e.m.i. data dalla (3), applicando il secondo principio di Kirchhoff alla maglia si ha, trascurando la resistenza dell’avvolgimento e quindi la c.d.t. relativa:
![]()
![]()
il cui il valore massimo o ampiezza è
![]()
Passando ai valori efficaci
![]()
Si ricordino infatti le relazioni, fra i moduli
, che legano valore efficace e massimo in regime sinusoidale:
![]()
Per la (6) la tensione U deve quindi controbilanciare la –E .
La tensione U fornita dal generatore, tenendo conto della sua posizione nel piano di Gauss come evidenzia la fase della (5) si può scrivere, in valore efficace e per le note considerazioni sull’operatore ‘j’ citate in precedenza:
![]()
Il vettore tensione U, per la (5) e per la (7), è dunque in anticipo rispetto alla corrente, proprio perché deve essere opposto al vettore f.e.m.+E.
Definendo in particolare come reattanza induttiva XL il prodotto
![]()
la caduta di tensione ai capi della bobina ideale si scrive:
![]()
In altro modo si può osservare che il prodotto XLI ha le dimensioni di una c.d.t., in cui l’ostacolo è la reattanza induttiva XL percorsa dalla corrente.
Questa “resistenza” particolare è in realtà un ostacolo che, percorso da corrente, crea ai capi della bobina ideale una caduta di tensione che anticipa di 90° la posizione del vettore corrente.
Se si ricorda infatti il carattere inerziale della induttanza, ovvero della grandezza che ostacola le variazioni di corrente, questo ostacolo viene attribuito alla reattanza, che congloba, oltre alla induttanza, anche la frequenza.
Infatti con più rapide variazioni della corrente aumenta la difficoltà da parte della corrente a percorrere il circuito induttivo.
In particolare con frequenza nulla è nulla anche la reattanza, mentre con frequenza crescente cresce linearmente anche la reattanza, fino a diventare infinita con frequenza infinita.
- In corrente continua (f=0) la reattanza è un corto circuito;
- con frequenza infinita la reattanza è come un interruttore aperto.
Si conclude ricordando che a regime (esaurita quindi la fase transitoria il cui studio non è qui riportato) una induttanza ha la proprietà di ritardare di 90° la corrente che l’attraversa rispetto alla caduta di tensione esistente ai suoi capi.
In modulo e in valore efficace tale corrente è il rapporto fra la tensione efficace ai suoi capi e la reattanza induttiva XL=ωL .
Alla reattanza induttiva si attribuisce quindi la scrittura
![]()
utile nelle applicazioni con il metodo simbolico.
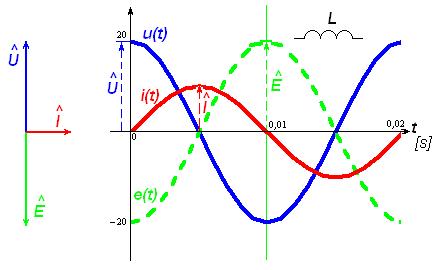
Figura 4)
Diagrammi vettoriale e temporale riferiti ad un circuito puramente
induttivo in regime sinusoidale.
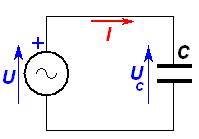
Figura 5) Circuito puramente capacitivo
Si prende ora in esame un condensatore ideale (trascurandone quindi eventuali effetti resistivi dovuti alle perdite nel dielettrico e induttivi, di per sé già trascurabili) ai capi del quale si imprime una tensione sinusoidale
![]()
Si ricorda che, quando si applica una tensione ai capi di un condensatore inizialmente scarico, si ha un movimento immediato degli elettroni dall’armatura resa positiva dal generatore fino a raggiungere l’altra armatura che acquista così il potenziale negativo.
Ad esempio nel processo di carica di un condensatore
alimentato da una tensione continua, poniamo di 10V, immediatamente gli
elettroni migrano dall’armatura positiva verso quella negativa e il processo
di migrazione continua fino alla carica completa del condensatore, cioè quando
fra le armature si stabilisce una d.d.p. praticamente uguale alla f.e.m. del
generatore. Durante la carica il processo di migrazione viene rallentato dal
potenziale che man mano cresce ai capi del condensatore stesso.
Qui non si considera la fase transitoria e si
ragiona come se essa si fosse già esaurita.
Se la tensione alternata ai capi del condensatore varia secondo la (8), in modo sinusoidale, il legame fra la variazione di tensione, la variazione di carica e la corrente di spostamento vale, essendo
q=icּt=Cּuc:
![]()
Pertanto la corrente che interessa il circuito formato dal generatore, dal condensatore e dai collegamenti (di resistenza trascurabile anch’essi) si calcola, dalla (9) e tenendo conto della (8):
![]()
Ricorda che
![]()
Dalla (10) si deduce che la tensione impressa ai capi del condensatore e la
corrente che interessa il circuito capacitivo puro sono a 90° fra loro: la
tensione è in ritardo rispetto alla corrente (è lo stesso dire che la corrente
anticipa la tensione impressa di 90°).

Figura 6) Diagrammi vettoriale e temporale riferiti ad un circuito puramente capacitivo alimentato con tensione sinusoidale.
Dall’andamento temporale della tensione e della corrente a regime in un circuito capacitivo puro (fig.6) si osserva che:
· quando il condensatore è scarico (uc=0) in quell’istante la corrente è massima;
· quando la tensione comincia a crescere si ha la carica del condensatore;
· il condensatore è carico quando la tensione ai capi è massima (corrente nulla);
· nell’intervallo di scarica la tensione ai capi diminuisce passando dal valore massimo a zero, mentre la corrente cresce da zero al valore massimo;
· nel semiperiodo negativo della tensione si ripetono l’analoga fase di carica e di scarica.
· Con tensione decrescente la corrente aumenta e viceversa con tensione crescente.
Si riprende in esame la (10).
L’ampiezza della corrente (il valore massimo) è:
![]()
Passando ai valori efficaci e
definendo la reattanza capacitiva
![]()
dalla (11) si ottiene la relazione fra i moduli della tensione e della corrente in un circuito puramente capacitivo:
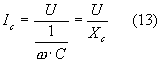
La reattanza capacitiva Xc
torna utile per considerare l’ostacolo che il condensatore offre al movimento
delle cariche. Essa ha qui la proprietà di creare una speciale c.d.t. ai capi
del condensatore percorso da corrente, speciale nel senso che è sfasata in
ritardo di 90° rispetto alla corrente (oppure, ovviamente, la
corrente è in anticipo di 90° rispetto alla c.d.t. ai capi del condensatore
stesso).
Pertanto alla reattanza capacitiva, nel calcolo con metodo simbolico, si attribuisce l’una o l’altra delle espressioni equivalenti
![]()
La (13) quindi va scritta con la seguente rappresentazione simbolica:
![]()
ovvero per rappresentare la c.d.t. ai capi del condensatore, legata alla corrente circolante:
![]()
La reattanza capacitiva decresce dal valore teorico infinito con frequenza nulla (ad esempio in corrente continua, per f=0, cessato il transitorio di carica, non vi può essere ulteriore movimento di cariche).
Al crescere della frequenza la
reattanza diminuisce sempre più fino ad annullarsi con frequenze altissime.
Pertanto si può semplicemente affermare che
un condensatore con frequenze altissime si comporta come un corto circuito;
con frequenza nulla si comporta come un interruttore aperto.
Da ricordare
Vi è dualità fra:
- il circuito induttivo puro in cui l’induttanza L ostacola le variazioni di corrente (questo può servire a ricordare che la corrente è in ritardo di 90° rispetto alla tensione impressa ai suoi capi) e
- il circuito con capacità pura C, che ostacola le variazioni di tensione : si ricorda così che la tensione ai capi ritarda di 90° la corrente (o che la corrente anticipa l’andamento della tensione di 90°).
Il perché lo sfasamento sia di 90° è dimostrabile col calcolo differenziale.
Osservazione
importante
In seguito, nei calcoli e nelle rappresentazioni con i vettori associati a grandezze sinusoidali, non si farà più riferimento all’ampiezza del vettore, ma si intenderà rappresentarne il valore efficace, che è quello comunemente sottinteso nelle applicazioni.
Quando si parla di una corrente di 2A o di una tensione di 230V ci si riferisce infatti al valore efficace della grandezza in esame e pertanto anche il vettore che la rappresenta avrà il modulo coincidente con il valore efficace, anziché col valore massimo.
Le grandezze suddette sono ritenute sinusoidali: la quasi totalità dell’energia elettrica è prodotta e distribuita con questo andamento temporale (salvo poi eventualmente convertirla in continua).
Si osserva ancora che, nelle rappresentazioni vettoriali e nelle equazioni, il vettore potrà essere espresso con la lettera che lo rappresenta, sormontata dalla tipica frecciolina, come nelle equazioni di fig. 7, oppure da una lineetta al posto della freccia, o la scritta in grassetto:
![]()
Più spesso si ricorrerà alla scrittura in grassetto.
Addirittura nei diagrammi vettoriali si intenderà che le grandezze presenti siano, appunto, dei vettori.
Nel prossimo paragrafo si generalizzerà il concetto di ostacolo al passaggio della corrente, mediante l’introduzione della impedenza Z.
10d_Elementi
passivi puri: schemi, diagrammi corrente-tensione
Nella fig.7 si riassumono le caratteristiche fondamentali dei circuiti semplici, con riferimento agli sfasamenti fra la corrente che li attraversa e la corrispondente caduta di tensione ai loro capi.

Figura 7) Schemi, rappresentazioni vettoriali ed equazioni riferite agli elementi passivi puri R - L - C. Negli schemi e nei diagrammi si farà riferimento ai valori efficaci di tensione e di corrente in gioco. L’ostacolo al passaggio della corrente in alternata è l’impedenza Z (v.§11)
![]()
prof. Attilio Barra e-mail: elettrotecnica@barrascarpetta.org
prof. Antonio Scarpetta e-mail: laboratorio@barrascarpetta.org
Indice generale Home Indice moduli