Indice generale      Elettro home      map      Indice moduli      Indice modulo 3

 M o d u l o  3

S i s t e m i   T R I F A S E

<<<==    <=    Unità  7

 

17_ Misura delle potenze nei sistemi trifase
 

       Si esaminano in questo modulo tutti i metodi di misura della potenza reale e reattiva su linee trifase e trifase con neutro, che basano la loro giustificazione sul teorema fondamentale seguente. Determinate le potenze si può risalire, per via indiretta, alla valutazione del fattore di potenza dell'impianto posto a valle del gruppo di misura.

 

1_ Teorema fondamentale delle potenze _ Inserzione ARON

    Per tensioni effettive si intendono quelle della terna U10’, U20’, U30’ di fig.1) che si trovano ad agire proprio ai capi di ogni singola fase e che partono dal centro effettivo 0’ e sono dirette ai potenziali fissi di riferimento 1,2,3.

    La terna delle tensioni baricentriche è quella simmetrica formata dai vettori U10, U20, U30 con centro il centro stella ideale 0, che è anche il baricentro del triangolo delle tensioni concatenate avente i vertici nei punti 1,2,3.

    Si discute, qui di seguito, il caso particolare di sistema trifase a 3 fili, ma il discorso si potrebbe estendere al caso generale di sistemi polifase.

    Si immagini un sistema trifase senza neutro, con carico squilibrato a stella. Ai capi di ogni fase agisce una tensione non baricentrica, ma quella che è riferita al potenziale spostato 0’ del centro stella (v. teoria spostamento centro stella al §12).

Figura 1) La potenza totale del carico trifase non cambia, sia che agiscano le tensioni effettive (riferimento delle tensioni in 0’, sia che il riferimento sia il centro stella isolato 0, immaginando di spostare parallelamente a sé i vettori delle correnti, qui non riportate. Cambiano però le singole letture, ma non la loro somma.

    Per il sistema di fig.1) si dimostra quindi che la potenza attiva non cambia se si scambia la terna delle tensioni effettive con quella delle tensioni baricentriche (e viceversa).

    Partendo dall’espressione di Boucherot applicata al carico squilibrato di figura e successivamente ricordando dalla teoria del §12 che

la potenza attiva totale, cioè la somma delle singole potenze di fase, misurabili ognuna con un wattmetro inserito come in figura, si modifica come segue:

    Sviluppando i prodotti ed essendo

si scrive:

e si conclude che la potenza totale del sistema in esame rimane la stessa, anche se si usano le tensioni ideali della stella simmetrica. Naturalmente cambiano i valori parziali, ma il risultato finale non muta. Quindi:

    La stessa dimostrazione si può ripetere anche per la potenza reattiva totale del carico trifase.

    D’ora in poi si possono scrivere indifferentemente le due espressioni, dimostratesi identiche, senza necessità di precisare se le tensioni sono quelle della stella ideale o sono quelle effettivamente disponibili ai capi delle singole fasi:

    Il teorema consente dunque di prendere come riferimento delle tensioni delle bobine dei wattmetri il potenziale del filo neutro e, se questo non esiste, del centro della stella equilibrata formata dalle resistenze identiche interne delle stesse voltmetriche dei wattmetri (naturalmente se i tre strumenti possiedono identiche caratteristiche costruttive). Quindi, con riferimento alla fig.1), la potenza attiva totale non cambia sia che esista, o no, il collegamento fra i due centri stella. Possono cambiare le indicazioni parziali, ma non il risultato finale.

    In particolare, se il centro di riferimento delle tensioni 0’ fosse preso su un filo qualsiasi, ad esempio il filo 3, il punto 3 diventerebbe il nuovo riferimento per le tensioni (3≡0’) e sostituendo

la potenza totale del carico diventa

e infine, ricordando che

si ottiene la relazione conclusiva

    I due prodotti scalari offrono la possibilità di essere interpretati come le indicazioni di due wattmetri elettrodinamici, inseriti come in fig.2), con le ampermetriche sui fili 1 e 2 e le voltmetriche tra i fili 1-3 e 2-3 rispettivamente.

    Si ricorda ancora che il wattmetro esegue il prodotto scalare fra la tensione ai capi della voltmetrica e la corrente dell’ampermetrica, ovvero il prodotto fra i valori efficaci di tali grandezze e il coseno del loro angolo di sfasamento.

Figura 2) Inserzione ARON valida per sistemi trifase qualsiasi (simmetrici e asimmetrici, equilibrati e squilibrati). La potenza attiva totale è la somma algebrica delle potenze misurate dai due wattmetri.

    L’inserzione di fig.2 viene detta "inserzione ARON", dal nome dell’ingegnere tedesco che la brevettò più di un secolo fa (1891) e che è attuale ancora oggi. E’ cambiata solo la strumentazione (analogica o digitale e la precisione), ma lo schema e la validità della teoria sono rimaste.

    Ancora si può generalizzare (teorema di Blondel) affermando che per la misura della potenza attiva totale in un sistema ad n fili sono sufficienti  n-1 wattmetri, se si sceglie su uno qualsiasi dei fili il potenziale comune di riferimento per gli equipaggi voltmetrici.

    Dagli schemi seguenti, anziché misurare le singole potenze di fase del carico prendendo come centro di riferimento delle tensioni il centro stella 0, si può assumere il riferimento sul filo 3 e così si risparmia pure un wattmetro ottenendo, come si è dimostrato, lo stesso risultato finale.

Figura 3) Evoluzione delle inserzioni: entrambe forniscono la stessa potenza totale, ma con Aron si semplifica la misura, con un wattmetro in meno. Il terzo wattmetro, con ingresso e uscita voltmetriche sullo stesso filo 3, sarebbe inutile.

 

 

2_ Misura di potenza attiva su sistemi simmetrici e carichi squilibrati

    E’ sempre valida l’inserzione Aron di fig.2 per linee a tre fili senza neutro.

    Per esse la somma vettoriale delle tre correnti di linea è nulla e i moduli delle tensioni concatenate Ulinea sono identici, essendo il sistema simmetrico.

    Le indicazioni dei singoli wattmetri sono le seguenti:

in cui le letture sono

    Ricordando che sulla voltmetrica del primo wattmetro agisce la U13 (opposta alla U31) e che l’angolo di ritardo delle tensioni stellate rispetto a quelle concatenate che interessano è di 30°, si giustificano le formule precedenti (fig.4). Per inciso si noti che, quando l’angolo tra la corrente e la corrispondente tensione concatenata supera 90°, la potenza del wattmetro acquista il segno negativo, essendo negativo il coseno dell’angolo.

Le relazioni (4) e (5) si possono applicare al calcolo delle letture dei wattmetri inseriti in Aron su una linea trifase con carico squilibrato.

Figura 4) Diagramma relativo ad un carico trifase squilibrato. Gli angoli in giallo sono gli sfasamenti che interessano le indicazioni dei due wattmetri in Aron. L’alimentazione è a tre fili e la somma vettoriale delle correnti di linea è nulla.

 

 

3_ Misura di potenza attiva su sistemi simmetrici e carichi equilibrati

    Per sistemi simmetrici e carichi equilibrati anche le correnti di linea hanno lo stesso modulo Il e lo stesso sfasamento φ rispetto alle tensioni di fase della terna stellata di riferimento. Per questi motivi le relazioni (4) e (5) si possono scrivere

    Eseguendo la somma delle due espressioni e sviluppando, tenendo sempre presenti le formule di sottrazione e addizione del coseno:

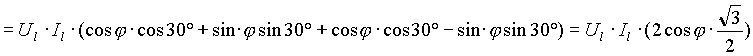
si ottiene infine

    La (8) conferma in altro modo, perché già si sapeva dalla (3), che la somma algebrica delle letture dei due wattmetri in Aron dà la potenza attiva del carico equilibrato nella forma più usuale già nota.

 

 

3a_ Misura della potenza reattiva per carichi equilibrati

    Eseguendo ora la differenza fra le due letture dei wattmetri inseriti in Aron e ricordando le formule di sottrazione e addizione degli archi della trigonometria:

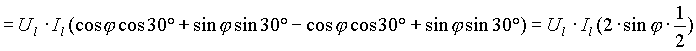
    Da cui si elabora

 

    La potenza reattiva di un carico trifase equilibrato si misura dunque attraverso l’inserzione Aron, moltiplicando per 1,732 la differenza algebrica delle letture dei due wattmetri inseriti in Aron.

    Si sottolinea che la determinazione della potenza reattiva mediante la (9) è valida solamente per carichi trifase equilibrati.

 

 

4_ CASI PARTICOLARI dell’inserzione Aron.

    Per carichi equilibrati e carichi con prevalenza non capacitiva, si possono evidenziare alcuni casi particolari:

· φ = 0° (carico resistivo puro)

    La (6) e la (7) si semplificano

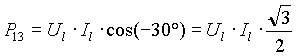
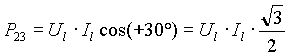
    Si hanno due letture identiche sui wattmetri.

 

· φ = 30° (carico R-L)

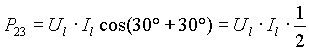
    Il wattmetro A (ovvero il P13 che ha la voltmetrica sul filo 1 e sul filo 3) misura il doppio del wattmetro B (ovvero il P23 che ha la voltmetrica sul filo 2 e sulla fase ciclica successiva 3).

 

· φ = 60° (carico R-L)

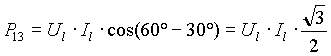
    Il wattmetro A misura tutta la potenza e si annulla la lettura del wattmetro B.

 

· φ = 90° (carico "L" puro)

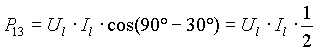
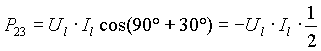
    Il wattmetro A misura la stessa potenza del wattmetro B, ma il segno negativo di quest’ultimo porta a una potenza attiva totale nulla, come deve essere:

 

    Nel caso di carico R-L si può dunque concludere che il wattmetro A segna un valore maggiore di quello B, eccetto nel caso di φ = 0°. Per φ > 60° il wattmetro B dà indicazione negativa.

    La situazione si rovescia completamente, come si può facilmente verificare, quando il carico è invece a prevalenza capacitiva (R-C), e quindi con sfasamento avente per convenzione il segno negativo. Nelle precedenti relazioni basta infatti sostituire + φ con – φ.

 

 

5_ Altre inserzioni per la misura di potenza reale su linee a tre fili

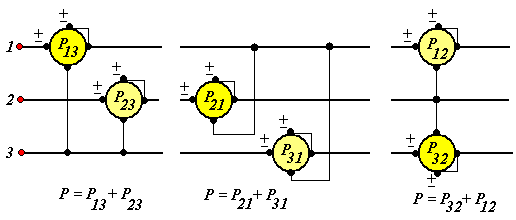
Figura 5) Inserzioni equivalenti, ottenute permutando ciclicamente gli indici.

    Nella fig.5) sono riportate le inserzioni possibili di Aron, fra loro equivalenti, come si può verificare dai diagrammi vettoriali o dalla dimostrazione (3). Basta infatti, a parità di senso ciclico delle fasi, permutare ciclicamente gli indici, da 1 a 2, da 2 a 3, da 3 a 1. Il wattmetro cosiddetto di "ponte maggiore", cioè il wattmetro A, è quello in colore più vivo.

    L’inserzione di tre wattmetri come in fig.1), consente la misura della potenza totale sommando le singole letture (con qualunque punto di riferimento comune per le uscite voltmetriche, anche un punto isolato). Tuttavia è più comoda e più conveniente l’inserzione Aron, che fa risparmiare un wattmetro.

    Con carichi equilibrati, anziché adottare lo schema di fig.1), è possibile inserire un solo wattmetro, mediante un centro stella artificiale, costituito da due resistenze esterne di valore ohmico coincidente con quello della resistenza voltmetrica del wattmetro, secondo lo schema di fig.6). Il potenziale comune è il centro stella ideale, ovvero il baricentro 0. La potenza totale si ottiene con la relazione:

P = 3 U10 I1 cos φ = 3 · P10           (10)

in cui P10 è la potenza di una fase del carico, che si deve conoscere come equilibrato.

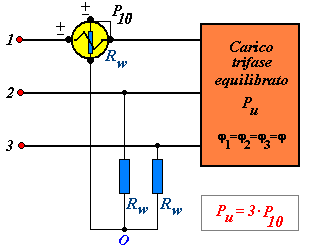
Figura 6) Misura di potenza con centro stella artificiale. Le due resistenze esterne hanno un valore ohmico identico alla resistenza interna della bobina di tensione del wattmetro.

 

 

6_ Misura di potenza attiva su linea trifase con neutro (4 fili)

6a)_ Inserzione di tre wattmetri con riferimento sul neutro _ Costante di un wattmetro

    Per un sistema trifase e neutro si ricorre all’inserzione di fig.7), con morsetto comune di uscita sul filo neutro. La potenza attiva totale è quindi

P = P10 + P20 + P30                  (11)

    Se il riferimento fosse scelto su un filo di linea, vi sarebbero due wattmetri con bobina voltmetrica sottoposta alla tensione concatenata e il wattmetro con l’ampermetrica sul neutro sarebbe invece sottoposto alla tensione stellata. Come complicazione si avrebbero costanti diverse per le letture, perché diverse dovrebbero essere le portate delle bobine voltmetriche.

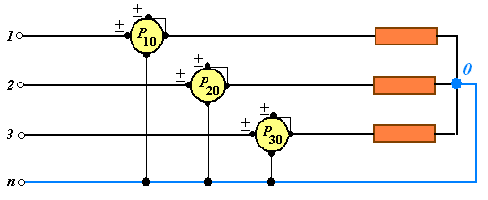
Figura 7) Misura di potenza reale con sistema a tre fili e neutro: P=P10+P20+P30

 

COSTANTE DI UN WATTMETRO

    Si ricorda che la lettura di un wattmetro analogico è il prodotto della costante strumentale KW e delle divisioni ΔW lette sulla scala graduata.

    La costante a sua volta si calcola tenendo conto delle scelte fatte per le portate della bobina ampermetrica "I", percorsa dalla corrente di linea e della portata della bobina voltmetrica "U" scelta in base alla tensione presente ai suoi capi. La costante è data dal prodotto delle portate e del fattore di potenza di taratura cosφT che viene fornito dal costruttore. Normalmente questo valore è unitario.

    Ad esempio, se si sono scelte le portate di 5A e 300V e le divisioni di fondo scala sono 150, la costante dello strumento è:

 

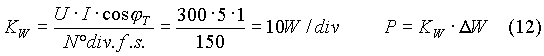
6b)_ Inserzione con strumento a doppia ampermetrica per sistemi a 4 fili

    Disponendo di un wattmetro con doppia ampermetrica o con analoga strumentazione elettronica si può anche ricorrere all’inserzione di fig. 7a), in cui i prodotti scalari dei due strumenti, sommati algebricamente, forniscono la potenza attiva del sistema trifase con neutro. Infatti:

ed essendo

si ottiene, dalla somma delle due letture, la potenza attiva totale del carico:

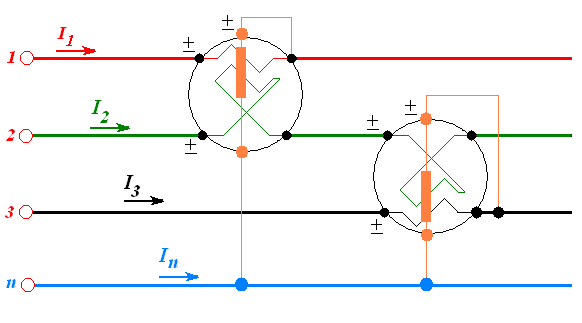
Figura 7a) Inserzione per la misura di potenza reale con strumenti a doppia ampermetrica.

 

 

7_ Osservazione sulla potenza istantanea, di fase e totale di un sistema

    Tutti i sistemi polifase simmetrici ed equilibrati hanno una potenza complessiva che si mantiene rigorosamente costante nel tempo, senza alcuna ondulazione. Per questo motivo si passa ad esempio da alimentazione trifase a bifase quando si hanno due carichi identici. Alimentati in trifase costituirebbero un carico squilibrato, mentre si deve tendere ad equilibrare il più possibile le correnti dei sistemi, per evitare la dissimmetria causata dalle diverse c.d.t. in linea. Alimentando invece i due carichi uguali con un sistema bifase (due tensioni di ugual ampiezza e sfasate di 90°), la potenza totale resta in tal caso costante sempre, senza alcuna pulsazione della potenza totale essendo, per la linea, il carico alimentato di tipo equilibrato.

    In fig.8) sono riportati gli andamenti temporali delle potenze istantanee di ogni fase, relativamente ad una alimentazione trifase e ad un carico trifase equilibrato, con le seguenti caratteristiche:

    Con questi dati si sono costruite le curve di figura.

    Essendo elevato il f.d.p. dell’esempio (cosφ=0,928) la parte negativa delle potenze istantanee è molto ridotta. Si noti però che le tre potenze istantanee hanno ugual ampiezza. Inoltre la potenza attiva totale, loro somma istante per istante, è rigorosamente costante ed assume il valore fisso di 4,37kW (essendo costante, banalmente coincidono valore medio, massimo e istantaneo!).

    Inoltre la frequenza delle potenze istantanee è doppia rispetto alla frequenza di 50Hz del sistema di alimentazione (se f=50Hz il periodo è T=20ms).

 

Figura 8) Andamento delle potenze istantanee di fase (f=100Hz, doppia rispetto a quella di tensione e corrente) e della potenza totale p(t). Se il carico è equilibrato come nel caso in esame, la potenza totale, somma delle potenze istantanee, rimane costante nel tempo (linea rossa).

    Diversamente si può verificare (fig.8a) che con carichi squilibrati la potenza complessiva p(t) non è più costante, ma pulsa tra un valore minimo e uno massimo due volte ad ogni periodo della corrente.

    Si riportano di seguito i risultati conclusivi, che si invita a verificare come applicazione, relativi ai seguenti dati di una linea trifase con neutro e carico squilibrato.

 

 

Curve della potenza istantanea - Esempio numerico

    Una linea trifase alimenta alla tensione concatenata di 400V (valore efficace) e frequenza 50Hz, un carico squilibrato a stella con neutro, i cui dati delle impedenze sono riportati in tabella.

R1

[Ω]

X1

[Ω]

R2

[Ω]

X2

[Ω]

R3

[Ω]

X3

[Ω]

10

60

20

40

50

0

 

Ulinea

[V]

IL1

[A]

IL2

[A]

IL3

[A]

In

[A]

P1

[W]

P2

[W]

P3

[W]

PT

[W]

QT

[var]

400

3,797

5,164

4,619

6,863

144

533

1067

1744

1932

    I risultati riportati sopra rappresentano valori efficaci per tensioni e correnti, per la P i valori medi, come si è detto più volte.

    Nelle curve di fig. 8a) sono rappresentati i valori istantanei delle potenze di fase p1(t), p2(t) e p3(t) e i rispettivi valori medi P1, P2, P3. La curva della potenza istantanea, somma delle singole potenze istantanee ptot(t), in rosso, è variabile, diversamente dal caso precedente di carico equilibrato. Il valor medio PT della potenza istantanea totale si deduce dal calcolo

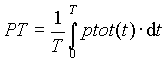
    Ma lo stesso risultato coincide con il calcolo seguente delle singole potenze e con la successiva applicazione del teorema di Boucherot, nel solito modo (p.e. con R·I2, oppure con UIcosφ), ovvero

PT = P1 + P2 + P3

(e si ottiene il valore costante pari a 1744W di fig. 8a).

    Tutte le curve delle potenze istantanee hanno frequenza doppia di quella di rete, come si è già verificato più volte e cioè frequenza di 100 Hz. Si ricorda che per la rappresentazione temporale le ampiezze, essendo le grandezze sinusoidali,  sono legate ai valori efficaci dalla relazione

    In fig.8b) sono riportate, in funzione del tempo (periodo della tensione T=20ms), le tensioni stellate e le correnti di linea, nonché quella del neutro.

Figura 8a) Potenze in funzione del tempo, nel caso di carico trifase squilibrato. Nella figura in basso 8b) sono rappresentate le tensioni stellate e le correnti di linea e nel neutro.

 

Figura 8b)

 

 

8_ Misure della potenza reattiva _ Generalità

 

    Se si ha un sistema dissimmetrico e squilibrato a 3 fili la potenza reattiva totale si ricava, al solito, dal teorema di Boucherot delle potenze, sommando algebricamente le potenze reattive di ogni fase del carico:

    (Ricorda che l’operatore -j applicato ad un vettore lo fa ruotare di 90° nel senso dei ritardi. Pertanto, ad esempio, l’angolo fra i vettori –jU1 e la rispettiva corrente di fase I1 è 90°-φ1 e quindi si giustifica la scrittura precedente).

    In base al teorema generale visto sopra (§1), anche per le potenze reattive si può dimostrare che

in un sistema polifase la potenza reattiva totale non cambia se si sostituiscono le tensioni effettive con quelle baricentriche.

    Pertanto all’espressione generale (13) si può sostituire la seguente, equivalente come risultato finale, ma ottenuta usando le tensioni baricentriche.

    Questa relazione torna spesso comoda, specie quando non si conoscono le tensioni effettive.

    Per la misura della potenza reattiva si possono impiegare dei varmetri, del tipo a induzione, elettrodinamici e elettronici. Più spesso si utilizzano ancora i wattmetri elettrodinamici, con inserzioni particolarmente adatte per il tipo di sistema in esame.

    Va detto che è indispensabile, prima di procedere all’inserzione degli strumenti, conoscere il senso ciclico delle fasi, onde non pregiudicare la correttezza delle indicazioni. Si pensi ad esempio che scambiare un ingresso con un’uscita significa cambiare il verso di un vettore, con risultati finali che altererebbero la misurazione.

 

8a_ Sistemi dissimmetrici e squilibrati a 3 fili

Valgono le considerazioni fatte per i wattmetri elettrodinamici, qui riferite invece ai varmetri (misuratori di potenza reattiva). Nel caso più generale possibile del sistema in esame, si può ricorrere all’inserzione Aron di due varmetri sommandone algebricamente le letture:

Q = Q13 + Q23                     (16)

Occorre rispettare rigorosamente il senso ciclico delle fasi, per poter procedere ad una corretta inserzione.

 

8b_ Sistemi simmetrici ed equilibrati

· Inserzione Aron di due varmetri

Vale la relazione (16) scritta sopra.

· Inserzione di un wattmetro elettrodinamico in quadratura.

    Con riferimento alla fig.9) il wattmetro è inserito con la bobina ampermetrica in serie al filo 3 (indicato come P’’’) e la voltmetrica ha l’ingresso sul filo 1 (ciclico successivo alla fase ’’’) e l’uscita sul filo 2 (ciclica successiva alla 1).

    Il termine "quadratura" è riferito alla posizione del vettore tensione di fase U30 (fase a cui è riferita la corrente nella bobina ampermetrica) rispetto alla tensione concatenata U12 agente sulla voltmetrica del wattmetro.

    Il prodotto scalare che esegue il wattmetro vale dunque

e per ottenere la potenza reattiva totale del carico trifase equilibrato si esegue il calcolo

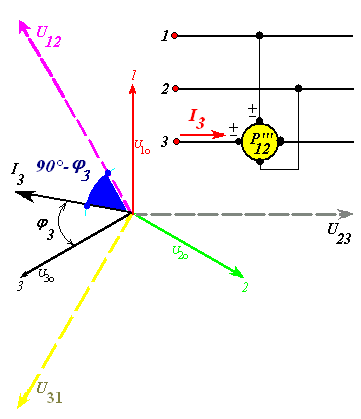
Figura 9) Inserzione di un wattmetro in quadratura. I pedici 12 si riferiscono all’ingresso e all’uscita della bobina voltmetrica; l’apice ’’’ indica la fase ampermetrica.

 

· Inserzione Aron di due wattmetri

    Lo schema è sempre quello di fig.2) e la dimostrazione è del §3a).

    Vale solo per carichi equilibrati.

 

    Si può verificare facilmente che le misure ottenute dal wattmetro in quadratura e la differenza tra le letture di Aron coincidono, ovvero

 

8c_ Sistemi simmetrici e carichi squilibrati (con tre fili o con 3 fili + neutro)

    La misurazione della potenza reattiva nei sistemi trifase con carichi squilibrati è più complicata rispetto alla misura di potenza attiva, che si svolge sempre con inserzione Aron.

    Un esempio tipico di applicazione si ha nel collaudo di un trasformatore trifase. Nel funzionamento a vuoto, infatti, la macchina si comporta come un carico squilibrato, a causa della dissimmetria magnetica, che influenza solo questo tipo di funzionamento (a carico le correnti di reazione elevate rispetto alle correnti assorbite a vuoto conferiscono un comportamento equilibrato alla macchina, sempre che al secondario sia allacciato un carico equilibrato).

    Vediamo i metodi di misura su linee trifase, partendo dall’inserzione di tre wattmetri in quadratura, perché dalla relazione conclusiva si possono far discendere le giustificazioni per le altre formulazioni.

 

· Tre wattmetri in quadratura

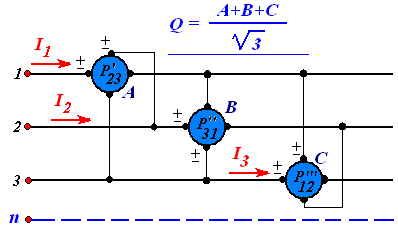
Figura 10) Inserzione dei wattmetri in quadratura, valida per linee a 3 fili e a 4 fili (con neutro)

    Come al solito è indispensabile conoscere il senso ciclico delle fasi.

    I tre wattmetri sono inseriti in quadratura: l’ampermetrica su un filo, l’entrata della voltmetrica sulla fase ciclica successiva e l’uscita sulla ciclica ancora successiva. In tal modo come si è già visto dal diagramma di fig.9, vi sono 90° fra la tensione di fase relativa all’ampermetrica e la tensione concatenata che agisce sulla bobina voltmetrica dei singoli wattmetri.

    Riprendendo il teorema delle potenze con la (15)

 

e in base alle relazioni seguenti, verificabili dalla posizione delle tensioni (v. fig.9 e ricorda che l'operatore "j " fa ruotare di 90° in anticipo il vettore su cui opera):

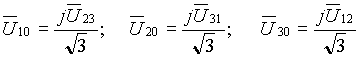
la (15) diventa, dopo semplici passaggi

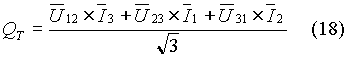
che sono le misure effettuate dai tre wattmetri in quadratura (chiamati più semplicemente C, B, A).

    Si può verificare che, con carico equilibrato, tutte le indicazioni coinciderebbero, sia con quella di fig.9, ovviamente, sia con la differenza algebrica delle indicazioni di due wattmetri in inserzione Aron.

    Il vantaggio di questa inserzione consiste nella possibilità di misurare anche la potenza reattiva totale in un sistema squilibrato con neutro.

    In sostanza l’inserzione vista si può utilizzare con linee a tre fili e a tre fili + neutro.

___________________________________________

· Inserzione Righi per sistemi simmetrici trifase (senza neutro) e carichi squilibrati

· Determinazione del fattore di potenza

    Si esamini lo schema d’inserzione di fig.11. Vi sono due wattmetri in inserzione Aron, che consentono anche la determinazione della potenza reale secondo la relazione

    La misurazione del terzo wattmetro, inserito in quadratura, si deduce dalla relazione generale (18).

    Partendo infatti da essa e sostituendo alle I1 e I2 le seguenti relazioni, valide per linee a tre fili:

si ottiene

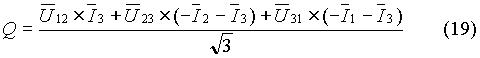
e sviluppando con semplici passaggi

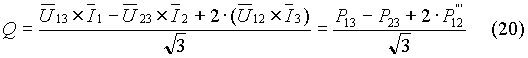
    Note la P e la Q si può determinare il fattore di potenza convenzionale del carico:

 

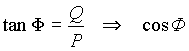
    Per l’inserzione occorre conoscere, come al solito, il senso ciclico delle fasi.

    Rispetto all’inserzione dei tre wattmetri in quadratura, "Righi" non si può impiegare per la misura di Q su linee con neutro, però consente la valutazione della potenza attiva totale P.

 

Figura 11) Inserzione Righi per sistemi simmetrici a tre fili e carichi squilibrati

___________________________________________

 

· Inserzione Barbagelata per sistemi simmetrici trifase senza neutro e carichi squilibrati

· Determinazione del fattore di potenza

    Lo schema deriva il nome dall’ing. Barbagelata che utilizzò quattro wattmetri per la misura, più in generale, su sistemi dissimmetrici e squilibrati. In fig. 12 lo schema a) è riferito a sistemi simmetrici a tre fili e carico squilibrato. La dimostrazione del Barbagelata seguì di alcuni anni quella di Aron, ma precedette quella del metodo Righi.

    Qui, semplicemente, partendo già dallo schema di fig.12, si può in effetti verificare che la differenza fra i due wattmetri in opposizione equivale all’indicazione del wattmetro in quadratura di Righi.

Infatti:

    Ovvero la differenza tra le indicazioni dei due wattmetri in opposizione equivale al "C" di Righi (P12’’’).

    Si ottengono dunque le espressioni conclusive per poter calcolare potenze e sfasamento del carico inserito a valle:

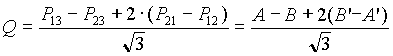
e per il fattore di potenza dell'impianto ci si avvale delle letture note di P e Q :

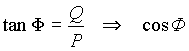
    La caratteristica di questo schema, pur richiedendo un wattmetro in più, come si è già accennato, è che ha  validità generale, che qui non verifichiamo.

    In particolare, per ridurre il numero di wattmetri, si può ricorrere all’inserzione di fig.12b):

    Occorre però raddoppiare le letture A’’ e B’’ a tasto aperto, perché le due bobine voltmetriche uguali sono in serie e quindi la lettura è dimezzata rispetto al valore che misurano i wattmetri A’ e B’ dell’inserzione completa.

               L’inconveniente di quest’ultima inserzione, che porta certamente ad un risparmio di due wattmetri (con quel che costano!), sta nella potenziale non affidabilità a causa della non contemporaneità delle letture. Passando da tasto chiuso a tasto aperto potrebbero modificarsi il carico e/o la tensione di alimentazione, falsando così il risultato finale.

 

Figura 12a) Inserzione Barbagelata con 4 wattmetri e schema semplificato in b).

 

 

N.B.) Per le misure di energia, eseguite con strumentazione analogica, si adottano gli stessi schemi d’inserzione esaminati nei paragrafi precedenti. Ovviamente, in sostituzione dei wattmetri, si impiegano i contatori, che integrano la potenza nel tempo.

          Dalle letture di energia reattiva e di energia attiva eseguite per la stessa durata si deduce il fattore di potenza medio mensile

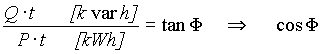
          Da questo risultato si ha la conferma o meno dell’efficienza del sistema di rifasamento.

 

prof. Attilio Barra e-mail: elettrotecnica@barrascarpetta.org

prof. Antonio Scarpetta e-mail:  laboratorio@barrascarpetta.org

 Indice generale      Elettro home      map      Indice moduli      Indice modulo 2

 

<<<==    <=        U n i t à    up