Indice
generale
Elettro
home
![]() map
Indice moduli
Indice
modulo 3
map
Indice moduli
Indice
modulo 3
M o d u l o 3
S i s t e m i T R I F A S E
POTENZE - Generalità
16_ Potenza istantanea _ Potenze attiva e reattiva – Grafici e definizioni _ Misura con wattmetri
Un utilizzatore monofase, ad esempio di tipo R-L (bipolo) è alimentato con tensione sinusoidale di pulsazione ω ed assorbe una corrente di cui si assumono le seguenti espressioni:
![]()
Con riferimento alla fig.1) si calcola la potenza istantanea:
![]()
Sviluppando e ricordando la formula di sottrazione del seno si ottengono le relazioni seguenti:
![]()
![]()
Per le note proprietà trigonometriche seguenti (bisezione e duplicazione), la (2) si modifica secondo la (3)
![]()
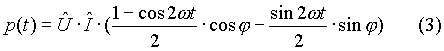
Svolgendo si ha ancora
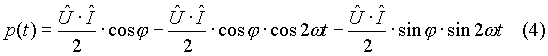
Dal legame tra valore massimo e valore efficace valido per grandezze sinusoidali si ha
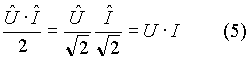
e la (4) diventa
![]()
Da questa, ponendo
![]()
(componente attiva della potenza)
e![]()
(componente reattiva della potenza)
si ottiene la potenza totale istantanea espressa per comodità dalla loro somma:
![]()

Figura 1) Curve della potenza istantanea riferite allo sfasamento tra u(t) e i(t), con le componenti attiva e reattiva: p(t)=pa(t)+qr(t). I valori costanti sono P e Q. Con i dati di figura si ottengono: P=(4·3/2)·cos60°=3W; Q=(4·3/2)·sin60°=5,2var. (v. fig.3 per sfasamenti variabili)
La potenza che ha significato fisico (perché è quella che viene dissipata in calore nella resistenza o è potenza meccanica in un motore) è la
·
potenza attiva o potenza reale, che è definita matematicamente come il valore medio della (6), cioè il valor medio in un periodo della potenza istantanea:
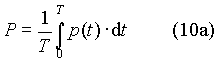
Eseguendo l’operazione precedente (ed osservando il grafico) si ricava il valor medio della potenza utilizzata e misurabile, che vale
![]()
essendo nulli i valori medi, in un periodo T, di cos2ωt e di sin2ωt.
·
La potenza reattiva non ha un analogo significato fisico, ma viene definita come
il valor massimo della componente reattiva della potenza istantanea [dalla rel. (8)]:
![]()
Si può osservare dai grafici che il valore medio del termine reattivo qr(t) è nullo, a confermare il fatto che questa potenza tiene impegnata la linea scambiandosi alternativamente fra utilizzatore e generatore e non è potenza persa.
·
Viene definita ancora una terza potenza, detta potenza apparente
S = U I [VA] (12)
Viene definita anche la potenza complessa che si valuta con l’espressione
![]()
in cui I* è il vettore complesso coniugato della corrente I, P è la parte reale e Q è il coefficiente dell’immaginario (v. applicazione di calcolo nel Tema 8).
La potenza P si dissipa nella resistenza R, la potenza reattiva Q (che non si dissipa ma si scambia continuamente) interessa le reattanze (segno + per le induttive e segno – per quelle capacitive); la potenza apparente S riguarda tutta l’impedenza Z ed è legata dal teorema di Pitagora alla P e Q (triangolo delle potenze di fig.2).

Figura 2) Triangolo delle potenze. La Q positiva è per convenzione attribuita allo scambio con +XL.
Le seguenti espressioni sono rappresentate in fig.1 per un bipolo R-L con costante di fase φ=60°:
- della tensione e della corrente istantanea (rel.1) (f=50Hz e ampiezze 4V e 3A),
- la (6) della potenza istantanea p(t) avente frequenza doppia (100Hz),
- la (7) della componente attiva della potenza istantanea,
- la (8) della componente reattiva della potenza istantanea
Sono inoltre riportati i valori costanti della potenza attiva P (rel.10) e della potenza reattiva Q (rel.11).
Dalla curva della potenza istantanea, fluttuante p(t) si osserva che vi sono intervalli di tempo in cui l’area sottesa (energia) è negativa, essendo la potenza anch’essa negativa. La parte positiva qui prevale su quella negativa e il valore medio è il valore costante P (valor medio), come si è visto analiticamente e, come area, è l’energia attiva consumata. La parte positiva è quella che va dal generatore all’utilizzatore (potenza e energia assorbite dal carico), quella negativa si riferisce alla potenza e all’energia che fluisce dal carico al generatore (restituita o generata).
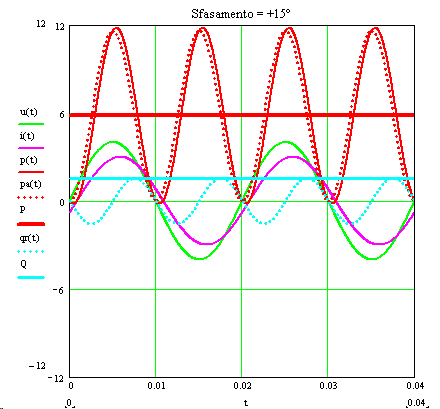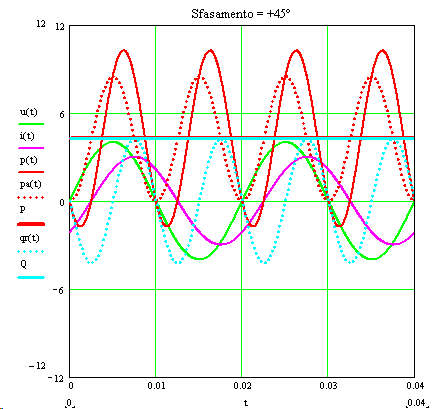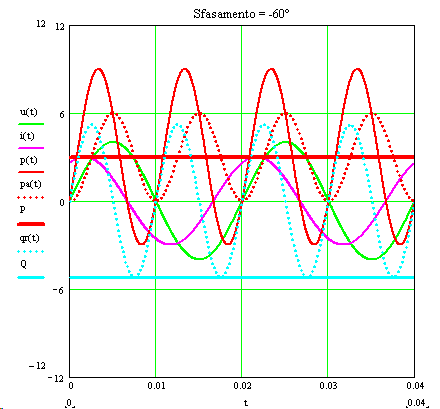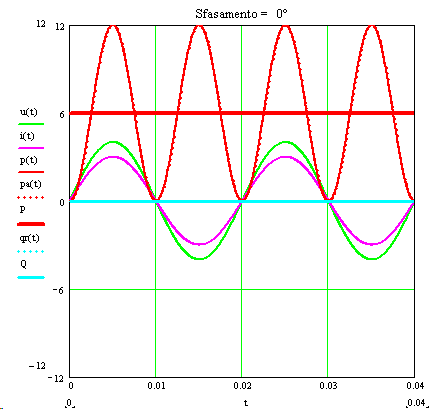
Figura 3) Successione dell’andamento dei grafici al variare dello sfasamento del carico (v. il caso particolare di fig.1).
La fig.3) mostra la successione delle curve già citate, per i vari sfasamenti, in ritardo e in anticipo, curve riferite al caso in cui frequenza, ampiezze e valori efficaci hanno i valori:
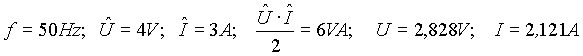
Si riassumono i dati salienti della figura:
- P : è il valor medio della potenza istantanea p(t); rispetto alle ascisse ha ordinata UIcosφ.
- Le aree positive sottese dalla potenza istantanea rappresentano energia assorbita dal carico, quelle negative sono restituite al generatore; l’effetto fisico è da attribuire al valor medio di p(t) che, come si nota anche dal grafico, si trova spostato di P, con valori positivi. Rispetto a tale linea presa come riferimento il valor medio sarebbe nullo.
- Il valore medio P è nullo solo per sfasamenti φ = ±90° (il carico non ha resistenza e quindi non dissipa potenza).
- La potenza reattiva è per definizione il valore massimo della componente reattiva della potenza istantanea. Come si vede anche dal grafico, Q è infatti l’ampiezza di qr(t), mentre il valor medio della componente qr(t) è nullo.
- P si può ricavare anche come valor medio della funzione pa(t), componente attiva della p(t), come si nota dal grafico.
- La potenza istantanea ha frequenza doppia rispetto a quella della tensione (e della corrente).
- In forma più concisa la (6) si può anche scrivere
___________________________________________
Valore medio del prodotto di due grandezze sinusoidali isofrequenziali
Più in generale, come conclusione importante deducibile dalla dimostrazione precedente, si può affermare che
il valor medio del prodotto di due grandezze sinusoidali di ugual frequenza è dato dal prodotto fra
- il valore efficace della prima grandezza,
- il valore efficace della seconda grandezza,
- il coseno dell’angolo di sfasamento fra i due vettori che le rappresentano.
Basti considerare, come si è dimostrato sopra:
la tensione e la corrente le due grandezze sinusoidali di ugual frequenza e il valor medio costante del loro prodotto dato dalla successiva relazione (14):
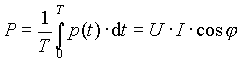
![]()
in cui φ è lo sfasamento fra i due vettori rappresentativi della tensione e della corrente e la scrittura concisa (la formula di mezzo) ne rappresenta il prodotto scalare, con il simbolo"X" che sostituisce il coseno dell'angolo fra i due fattori del prodotto.
![]()
IL WATTMETRO
Per la misura della potenza attiva di un bipolo si può inserire un wattmetro elettronico o lo strumento analogico più tradizionale che è il wattmetro elettrodinamico o, comunque, uno strumento che esegua il calcolo del valor medio del prodotto dei valori istantanei delle tensioni e delle correnti di ugual frequenza.
Lo strumento analogico elettrodinamico ha un equipaggio ampermetrico percorso dalla stessa corrente che fluisce nel carico e un equipaggio voltmetrico sottoposto alla stessa tensione agente sul carico. In seguito al principio di funzionamento che si basa sulle azioni elettrodinamiche delle due bobine, la coppia risultante, non potendo seguire i valori istantanei del prodotto fra tensione e corrente (di frequenza doppia della tensione), dipenderà dal valor medio del prodotto, ovvero dal prodotto fra i valori efficaci di tensione e corrente per il coseno del loro angolo di sfasamento.
Così si misura la potenza attiva che, come ripetuto più volte, è un valore medio, fisicamente significativo.
Lo strumento in questione dispone quindi di 4 morsetti, dei quali bisogna rispettare gli ingressi, onde evitare di far assumere alla misura il segno sbagliato (ciò è particolarmente importante per inserzioni su circuiti trifase).
In generale il costruttore evidenzia i cosiddetti morsetti d’ingresso con il segno ±, ad indicare che quei due morsetti dovranno avere un potenziale contemporaneamente maggiore o contemporaneamente minore rispetto alla coppia di morsetti non contrassegnati. Altri costruttori indicano una lettera, un asterisco * o un bollino ●, comunque riconoscibili come segnalazione di morsetti corrispondenti.
In altro modo si può pervenire al valore di P con una adatta strumentazione che esegua l'operazione di misura con il calcolo mediante la relazione (10a).
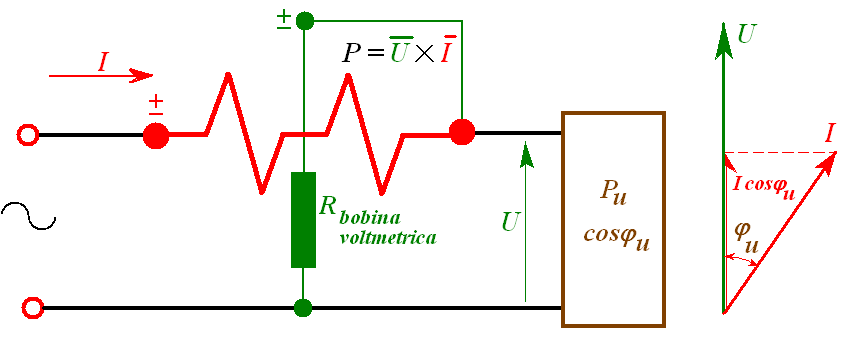
Figura 4) Inserzione di un wattmetro elettrodinamico che misura il valore medio della potenza P=UIcos
j u in cui j u è l’angolo caratteristico del carico. Occorre tener conto dei due morsetti contrassegnati dal costruttore per poter collegare correttamente lo strumento. Questa inserzione viene detta "a valle", perché la bobina voltmetrica è inserita "dopo", all’uscita dell’ampermetrica.prof. Attilio Barra e-mail: elettrotecnica@barrascarpetta.org
prof. Antonio Scarpetta e-mail: laboratorio@barrascarpetta.org
Indice
generale
Elettro
home
![]() map
Indice moduli
Indice
modulo 2
map
Indice moduli
Indice
modulo 2
<<<== <= U n i t à up => ==>>>