Indice generale      Elettro home      map      Indice moduli      Indice modulo 3

 M o d u l o  3

S i s t e m i   T R I F A S E

Unità  1    =>    ==>>>

 

DEFINIZIONI

 

      La generazione di un sistema trifase è riconducibile tipicamente all’alternatore, discusso come modulo della macchina sincrona (si veda http://www.barrascarpetta.org/01_ele/m_7/3_Ind_m7.htm).

        L’alternatore trifase genera tre f.e.m. identiche in modulo e sfasate di 120°, come è schematizzato anche nella seguente fig.1)

Figura 1) L’alternatore trifase genera le tre f.e.m. di fase, di ugual modulo e sfasate di 120°.

 

Figura 2) Terna delle tensioni di fase. Generatore trifase e carico, collegati a stella, sono allacciati alla stessa linea. Le correnti che percorrono le fasi generatrici e utilizzatrici coincidono con quelle di linea.

 

        Tra i vantaggi del sistema trifase rispetto al monofase si ricordano la migliore utilizzazione e convenienza applicativa delle macchine e degli impianti elettrici, la maggior facilità di trasporto e di conversione dell’energia, la possibilità di poter disporre di due terne di tensioni. Fra le macchine elettriche universalmente impiegate vi è il motore trifase (v. il modulo relativo alla macchina asincrona). Il sistema trifase crea infatti un campo magnetico rotante, che consente il funzionamento del motore citato.

Tensione di fase:

  • d.d.p. Ef esistente fra gli estremi di un singola fase generatrice,
  • oppure d.d.p. Uf di una singola impedenza utilizzatrice.

Tensione concatenata o tensione di linea EL, UL:

Ovviamente il vettore

è opposto rispetto a U12.

Figura 3) Terne simmetriche delle tensioni stellate e delle tensioni di linea. Per comodità nella risoluzione dei problemi la terna delle tensioni concatenate viene spesso riportata nel baricentro 0 del triangolo delle tensioni stesse.

Sistema simmetrico trifase:

quando le tensioni fornite da ogni singola fase del generatore hanno ugual modulo e sono sfasate di 360°/3 = 120°.

In tal caso anche la terna delle tensioni concatenate è simmetrica.

Figura 4) Come associare le sinusoidi ai vettori rappresentativi delle tensioni stellate e concatenate in un sistema simmetrico. Le terne di vettori ruotano in senso antiorario con velocità angolare costante ω (pulsazione) e riproducono, con la successione delle loro proiezioni, le rispettive funzioni temporali. In ogni istante la somma dei valori di ogni terna è sempre nulla. I vettori qui hanno una lunghezza pari al valore massimo (ampiezza), mentre di solito, nelle applicazioni, le terne di vettori si rappresentano con i valori efficaci. L’associazione dei vettori alle sinusoidi è un artificio utilissimo per poter affrontare i calcoli, ma non si dimentichi che le tensioni e le correnti sono comunque grandezze scalari, come lo è ad esempio la temperatura.

Sistema dissimmetrico o asimmetrico:

(riferito sempre alle tensioni), quando le tensioni non hanno ugual modulo e/o sfasamento.

Si considerano qui e nel seguito solo sistemi simmetrici, essendo spesso ininfluente il grado di dissimmetria per le usuali applicazioni di calcolo.

 

Corrente di fase:

corrente che percorre la fase generatrice o utilizzatrice.

Corrente di linea:

corrente che percorre la linea di alimentazione.

Carico trifase equilibrato:

le tre impedenze di fase sono identiche, con stesso modulo e stesso sfasamento caratteristico.

Carico trifase squilibrato:

quando una delle condizioni precedenti non è verificata

                                                (Esempio: tre impedenze hanno stesso modulo Z = 10 W , ma sfasamenti diversi)

Collegamento a stella (v.§5 e §6):

come si può dedurre ad esempio dal triangolo isoscele 023 di fig.3: la base 23 ha modulo

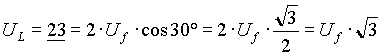
Collegamento a triangolo (v.§7):

 

Sistema trifase con neutro (v.§5 e §6):

            Come si chiarirà dalla risoluzione degli esempi proposti, il filo neutro non è percorso da corrente quando il carico trifase allacciato è equilibrato.

            Il filo neutro mantiene sempre immutato il modulo delle tensioni di fase, anche con carichi squilibrati e vale sempre la relazione

            La presenza di uno squilibrio del carico comporta invece il passaggio di una corrente nel filo neutro, nel quale si richiude la somma vettoriale delle correnti dei tre fili di linea. Si può dire che in tal caso il neutro costituisce il filo di ritorno della somma delle correnti dei fili di linea (somma dei loro valori istantanei o dei vettori ad esse associate).

 

Sistema trifase senza neutro:


 

1_ Trasformazione TRIANGOLO-STELLA e viceversa

            In alcune applicazioni può tornare utile ricordare che è possibile trasformare un triangolo in una stella equivalente e viceversa.

            In altre parole, se si ha un carico trifase collegato in una scatola chiusa e si eseguono misure di tensione, di corrente e di potenza esternamente ad essa, i valori delle grandezze non variano sia che all’interno il carico sia collegato a stella, sia che il carico sia disposto invece a triangolo, purché con impedenze tali da garantirne l’equivalenza (fig.5).

            Ad esempio, se si hanno tre impedenze identiche da 90 Ω ciascuna, collegate a triangolo, il loro comportamento equivale a quello di tre impedenze ancora fra loro identiche, ma collegate a stella con valore, in modulo, pari a 30 Ω e sfasamento identico a quello del carico di partenza.

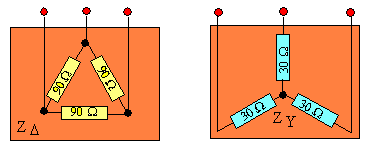
Figura 5) Circuito con carico equilibrato a triangolo, equivalente a quello a stella.

            Nella trasformazione, una fase della stella è 1/3 di quella del triangolo e ne conserva lo stesso sfasamento. I due schemi sono equivalenti.

            Questa conclusione è valida solo per carichi equilibrati, come in questo caso. Diversamente la determinazione dei valori equivalenti è complicata dal calcolo con metodo simbolico (si veda anche, come applicazione: §10 del modulo Il trasformatore).

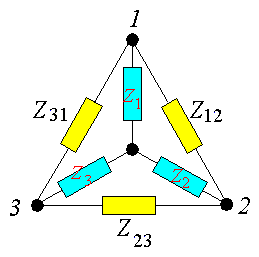
Figura 6) Trasformazione di un triangolo in una stella equivalente e viceversa. Caso generale.

            Le relazioni che si ottengono imponendo l’equivalenza tra i due schemi sono le seguenti, usando la simbologia di fig.6) e riferendosi al caso generale di impedenze qualsiasi.

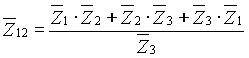
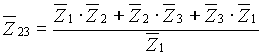
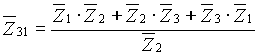
a) Trasformazione stella - triangolo (sono note le impedenze della stella):

Come caso particolare di carico equilibrato si ottiene

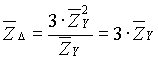
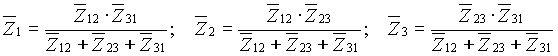
b) Trasformazione triangolo - stella (sono note le impedenze del triangolo):

Come caso particolare di carico equilibrato si ottiene

 

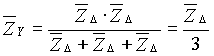
2_ Le potenze nel sistema trifase

Per il teorema di Boucherot relativo alle potenze e valido in qualunque sistema (monofase, polifase) si richiama la parte generale in

http://www.barrascarpetta.org/m_4/m4_u03tb.htm

Distinguiamo il caso di carico squilibrato e quello di carico equilibrato.

  • A) Carico trifase squilibrato

Si calcolano le potenze di ogni singola impedenza di carico e poi

1) si sommano numericamente le singole potenze attive per ottenere la potenza attiva totale PT del carico;

2) si sommano algebricamente le singole potenze reattive per ottenere la potenza reattiva totale QT del carico (col segno + i carichi R-L; col segno - i carichi R-C);

3) si sommano vettorialmente le singole potenze apparenti per ottenere la potenza apparente totale ST del carico. E’ possibile però determinarla più semplicemente col teorema di Pitagora.

Si può verificare che in presenza di carichi squilibrati la potenza istantanea complessiva non è costante, ma pulsa tra un minimo e un massimo due volte per ogni periodo della corrente. La potenza attiva del sistema è la potenza media in un periodo intero ed è la somma delle potenze reali delle singole fasi (v. il modulo di "Misura delle potenze").

in cui ΦT rappresenta l’angolo di cui occorrerebbe ruotare rigidamente la terna delle correnti rispetto a quella delle tensioni per ottenere la potenza attiva massima.

 

  • B) Carico trifase equilibrato

In particolare, quando il carico trifase è equilibrato, si possono fare le seguenti osservazioni:

a) collegamento a STELLA equilibrata:

la potenza attiva in una fase vale

e quindi, per il teorema di Boucherot, la potenza attiva totale sarà la somma di queste tre potenze:

Essendo inoltre, per il collegamento a stella

la (1) diventa

 

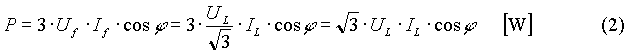
b) collegamento a TRIANGOLO equilibrato:

ricordando che con questo collegamento del carico si ha

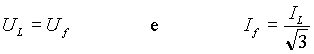
la potenza attiva totale diventa

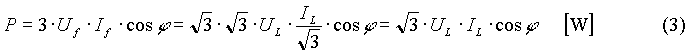
Come conclusione si può affermare che, per carichi trifase equilibrati, la potenza attiva totale si calcola indifferentemente con le due espressioni equivalenti:

 

La scelta va fatta in base alle preferenze, o ai dati noti del problema.

Di solito, essendo noti i valori di linea delle tensioni e delle correnti, è più usuale la relazione

valida per carico a stella o a triangolo, purché il carico sia equilibrato. Ovviamente tensione e corrente sono quelle di linea e cosφ è il f.d.p. del carico.

Le osservazioni precedenti valgono analogamente per le potenze reattiva e apparente:

 

Per la potenza apparente, con Boucherot, si può passare attraverso il teorema di Pitagora

 

  • Calcolo del fattore di potenza dell’impianto:

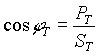
            Si osservi che, applicando qui la definizione data prima per carichi squilibrati, ruotando la terna delle correnti rispetto a quella delle tensioni dell’angolo φ, le correnti andrebbero in fase con le tensioni e la potenza attiva coinciderebbe con la potenza apparente, assumendone il valore massimo.

            A differenza di quanto accade per i carichi squilibrati, quando il sistema è simmetrico e il carico è equilibrato la potenza istantanea complessiva si mantiene assolutamente costante nel tempo, senza alcuna pulsazione (la potenza istantanea coincide quindi con la potenza media P del sistema, essendo nulla la potenza fluttuante) (v. il modulo di "Misura delle potenze").

 

2a_IL RIFASAMENTO

            Per migliorare il fattore di potenza di un impianto, posto ad esempio all’arrivo di una linea di alimentazione e per portarlo ad un valore cosφ’=0,9 imposto dall’ente distributore o a un valore più elevato, fino al rifasamento totale, occorre inserire in parallelo al carico una batteria di condensatori, che compensi parzialmente o totalmente quella di segno opposto del carico.

            Si osserva che, come non si deve scendere al di sotto del valore 0,9 imposto, non si può nemmeno rifasare in anticipo, onde evitare ad esempio problemi legati alla sopraelevazione della tensione di rete.

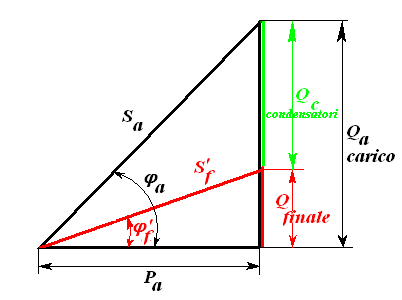
Figura 7) Diagrammi delle potenze dell'impianto utilizzatore prima e dopo il rifasamento.

            Per ridurre lo sfasamento complessivo dell’utenza e quindi per aumentare il fattore di potenza complessivo occorre inserire all’arrivo, in parallelo sul carico, una batteria di condensatori di potenza Qc.

Dalla fig.7 si ottengono le seguenti relazioni:

            La potenza reattiva che interessa una batteria di condensatori (con condensatori collegati a stella o a triangolo, ma tali da costituire un carico trifase equilibrato) si può anche determinare dalla relazione (9), essendo la reattanza capacitiva

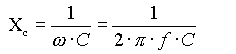
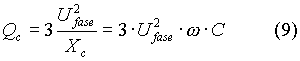
Dall’uguaglianza fra la (8) e la (9) si ottengono, a seconda del collegamento:

  • 1. collegamento a triangolo (Ufase=Ulinea=Ua):

da cui

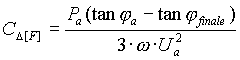
  • 2. collegamento a stella (Ufase = Ua / 1,732):

da cui

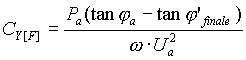
            In particolare si può notare che con il collegamento a triangolo la capacità di ogni fase è ridotta a 1/3 del valore a stella, e ciò può costituire un vantaggio relativamente al costo della batteria. Il costo però è anche condizionato dai problemi di isolamento, per cui con medie e alte tensioni si opta per il collegamento a stella, essendo la tensione di fase ridotta di 1,732 volte rispetto a quella di linea che agisce con collegamento a triangolo.

            In bassa tensione si opta invece per il collegamento a triangolo.
  • Vantaggi del rifasamento:

            L’aumento del f.d.p. in seguito al rifasamento porta alle considerazioni seguenti:

            Se l’utenza, rifasando, richiede minore potenza apparente, l’ente che eroga l’energia può soddisfare più utenze, rispetto a quando non si rifasa.

            Se un utente preleva dalla rete una potenza P e cosφ=1, mentre un secondo utente preleva la stessa P, ma con cosφ=0,5, la società che distribuisce l’energia deve fornire a quest’ultimo una corrente in ogni istante doppia rispetto a quella fornita al primo cliente, con maggiori perdite joule in linea e nelle macchine generatrici.

            Si ricorda ancora che la potenza attiva dell’utenza non viene modificata dalla presenza dei condensatori, ritenendo costante la tensione prima e dopo il rifasamento.

            Come collocazione ideale i condensatori dovrebbero essere posti dove è ubicato ogni singolo carico. In pratica però, a volte, si devono fare altre scelte per motivi di organizzazione, di costo, di gestione degli impianti e la condizione suddetta non viene sempre realizzata.

            Si può anche controllare in tempo reale il fattore di potenza dell’utenza e provvedere di conseguenza al rifasamento, in base alle mutate condizioni, mediante inseritori automatici di condensatori.

prof. Attilio Barra e-mail: elettrotecnica@barrascarpetta.org

prof. Antonio Scarpetta e-mail:  laboratorio@barrascarpetta.org

 Indice generale      Elettro home      map      Indice moduli      Indice modulo 2

 

U n i t à    up        =>    ==>>>