Indice
generale
Elettro
home
![]() map
Indice moduli
Indice
modulo 3
map
Indice moduli
Indice
modulo 3
M o d u l o 3
S i s t e m i T R I F A S E
RISOLUZIONE DI RETI TRIFASE
7_ Carico trifase squilibrato, collegamento a triangolo
Si esamina ora il caso del collegamento del carico a triangolo, che si può rappresentare con gli schemi equivalenti di fig.1 a) oppure di fig.b).

Figura 1) Collegamento a triangolo. I due schemi sono identici dal punto di vista funzionale. Lo schema b) è quello tipico delle morsettiere dei carichi a triangolo (p.e. motori).

Figura 2) Anche in questa figura i due schemi sono equivalenti dal punto di vista elettrico. I punti contrassegnati con lo stesso numero hanno lo stesso potenziale e pertanto si possono considerare coincidenti. Nei due schemi vi sono dunque i tre nodi
1, 2 e 3 , i cui potenziali sono quelli di fig. 3.Nel collegamento a triangolo le tensioni di fase coincidono con quelle di linea, mentre le correnti di linea derivano dall’applicazione del primo principio di Kirchhoff ai nodi: per carichi equilibrati, e solo per essi, la corrente di linea è maggiore di quella di fase secondo la relazione
![]()
Per le tensioni di fase si deve quindi fare riferimento alla posizione della terna delle tensioni concatenate e da esse dipendono le correnti di fase, secondo la legge di Ohm.
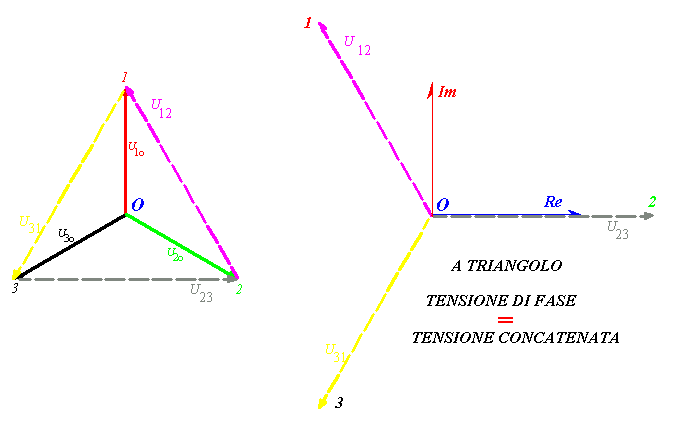
Figura 3) Qui sono rappresentate le terne delle tensioni stellate e concatenate. Per il carico a triangolo si deve fare riferimento alle tensioni concatenate o di linea, che sono anche le tensioni di fase per il collegamento in esame. La somma vettoriale delle tensioni concatenate è sempre nulla, essendo chiuso il relativo triangolo (vedi anche fig. 6).
Tema 3)
Una linea trifase alimenta, alla tensione concatenata di 390V, tre impedenze collegate rispettivamente fra i fili di linea 1-2, 2-3, 3-1:
![]()
Determinare le correnti di fase e di linea e tracciare il diagramma vettoriale tensioni-correnti.
Soluzione
Si fa riferimento agli schemi equivalenti di fig.2.
Si definiscono i versi delle correnti e generalmente si stabilisce che:
Conviene abituarsi a questa rappresentazione in successione ciclica dei pedici:
1-2; 2-3; 3-1… onde evitare di dimenticare che, se si attribuisse ad esempio il verso alla corrente in Z31 da 1 a 3, a produrla sarebbe la tensione U13 e non la U31, per cui occorrerebbe esprimerla sul piano di Gauss nella sua posizione corretta (opposta alla U31).
Si ricordi dunque che, stabilito il verso della corrente che va dal punto a verso il punto b, a produrla è la tensione generata Uab, e non la Uba (perché è il punto a che per convenzione ha il maggior livello elettrico).
Partendo dalla rappresentazione vettoriale delle tensioni di fase, si calcolano le singole correnti di fase, vettorialmente come si è detto e poi se ne determinano modulo e argomento. Gli angoli, riportati in gradi, sono riferiti all’asse reale (positivi in senso antiorario e negativi se percorsi in senso orario partendo dall’asse Re).
Si applica poi il primo principio di Kirchhoff ai nodi per poter calcolare le correnti di linea:
![]()
![]()
![]()
Si osservi la permutazione ciclica dei pedici, ottenuta stabilendo i versi alle correnti come consigliato sopra.
Eseguiti i calcoli col metodo simbolico, si posizionano i vettori delle tensioni e delle correnti sul piano di Gauss, verificando quindi che le correnti I12 e I23 sono in ritardo rispetto alla U12 e U23, mentre la I31 è in anticipo di 45° rispetto alla U31.
Le correnti di linea, in modulo, forniscono un’idea dello squilibrio complessivo del carico.
Si può ancora verificare, sempre per il primo principio di Kirchhoff applicato ai tre fili di linea, che la somma vettoriale delle tre correnti di linea è uguale a zero (vedi i grafici dei vettori e delle sinusoidi delle figg.5 e 6).

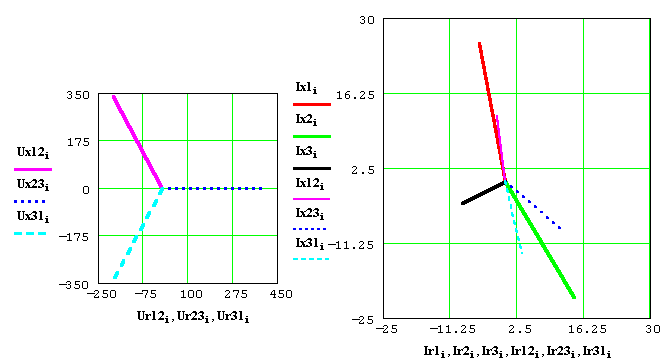
Figura 4) Diagramma delle tensioni e delle correnti, rappresentate con le componenti reali e immaginarie.

Figura 5) Tema 3: diagramma tensioni-correnti, con indicazione della fase di ogni impedenza di carico.
Come verifica si deve constatare che la somma vettoriale delle tre correnti di linea sia nulla. Per il carico a triangolo si può immaginare di applicare il primo principio di Kirchhoff ad una superficie chiusa che racchiuda il carico stesso. Questa superficie chiusa va intesa quindi come estensione di un nodo.
Per poter verificare questa operazione si esaminino i diagrammi temporali delle grandezze sinusoidali di fig. 6).
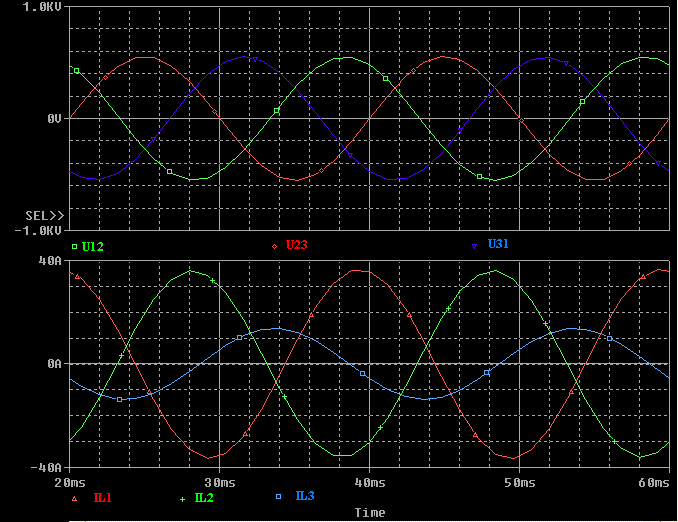
Figura 6) In alto le tensioni concatenate
u12, u23, u31. In basso le correnti di linea iL1. iL2, iL3. Si può agevolmente verificare che la somma, istante per istante, sia delle tensioni concatenate, sia delle tre correnti di linea, è nulla. Qui le sinusoidi sono associate ai vettori di fig.4) e di fig.5), con le ampiezze che sono naturalmente i valori efficaci dei vettori stessi moltiplicati per
![]()
8_Carico trifase equilibrato, collegamento a triangolo.
Lo stesso tipo di collegamento viene ora risolto nel caso in cui il carico trifase sia equilibrato, cioè formato da tre impedenze identiche.
Si confrontino successivamente le due diverse impostazioni.
Tema 4)
Una linea trifase alimenta, alla tensione concatenata di 390V, tre impedenze ohmico induttive identiche, ognuna di valore
![]()
collegate a triangolo, come in fig.2.
Si calcolino le correnti di fase e di linea e si esegua il diagramma vettoriale tensioni-correnti.
a) SOLUZIONE con il metodo vettoriale.
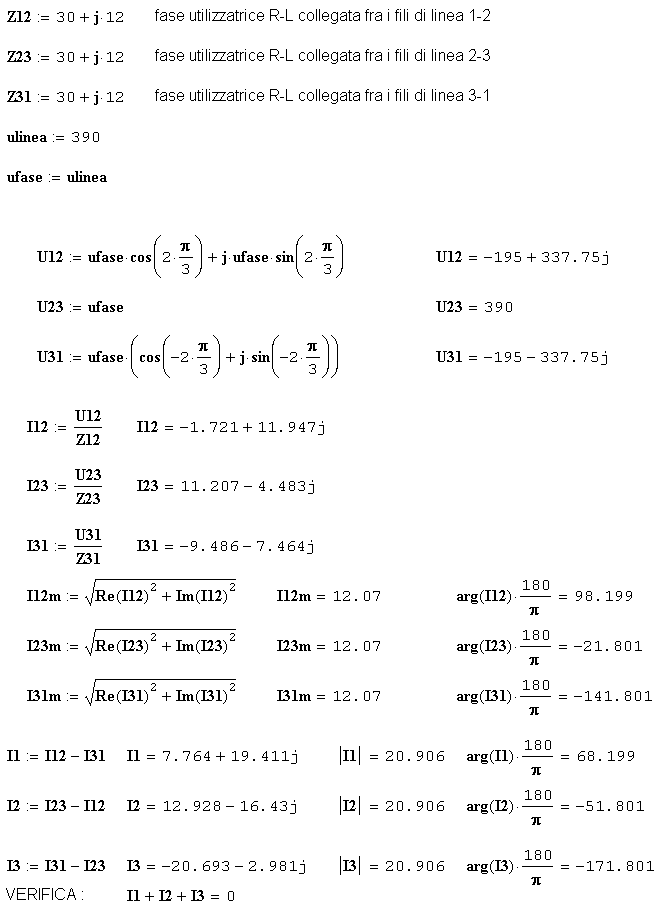
Questi risultati consentono di tracciare i diagrammi richiesti.
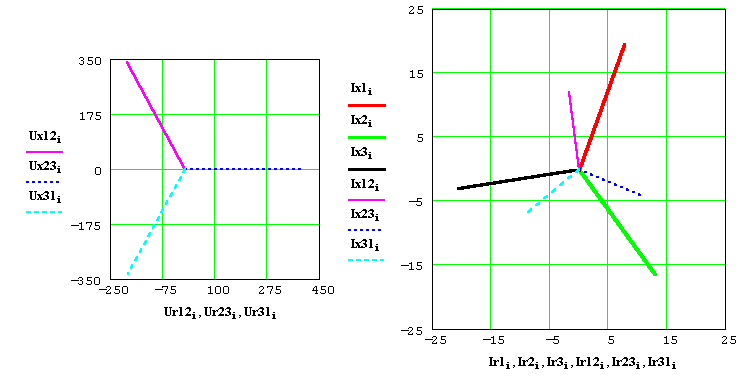
Figura 7) Componenti reali e immaginarie della terna delle tensioni e delle correnti
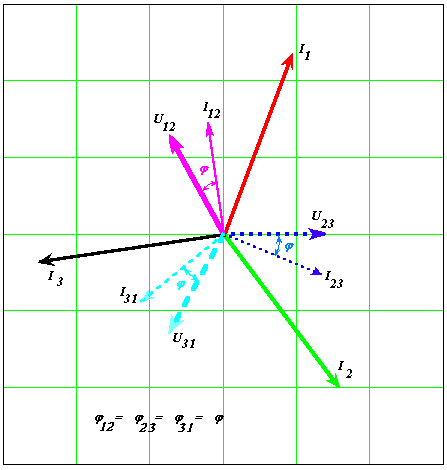
Figura 8) Diagramma completo delle tensioni e delle correnti di fase e di linea per carico equilibrato.
b) SOLUZIONE con il metodo numerico dei moduli
Dalle simmetrie di figura valide solamente per carico trifase equilibrato a triangolo, si può facilmente dedurre che, come si è fatto per le tensioni di fig.3, §1, il legame fra corrente di linea e di fase è il seguente
![]()
Il modulo di ogni corrente di fase è dato dal rapporto fra i moduli identici delle tensioni di fase, pari a 390V in questo esercizio, e il modulo delle impedenze
![]()
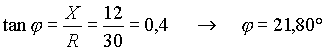
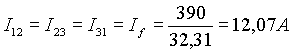
Ogni corrente di fase è in ritardo di j = 21,80° rispetto alla propria tensione di fase.
Le correnti di linea, per quanto appena affermato, valgono, in modulo:
![]()
e sono in ritardo di (30°+ j) rispetto alle tensioni.
Con carichi equilibrati i calcoli si semplificano notevolmente, ma non bisogna mai scordare che, pur in presenza di più carichi equilibrati connessi alla stessa rete, il calcolo della corrente assorbita totale proviene sempre da una somma vettoriale. In realtà, come si constaterà in esempi successivi (p.e. nel Tema 6), si potrà bypassarne il calcolo con il teorema delle potenze.
prof. Attilio Barra e-mail: elettrotecnica@barrascarpetta.org
prof. Antonio Scarpetta e-mail: laboratorio@barrascarpetta.org
Indice
generale
Elettro
home
![]() map
Indice moduli
Indice
modulo 2
map
Indice moduli
Indice
modulo 2