Indice
generale
Elettro
home
![]() map
Indice moduli
Indice
modulo 3
map
Indice moduli
Indice
modulo 3
M o d u l o 3
S i s t e m i T R I F A S E
RISOLUZIONE DI RETI TRIFASE
9_Circuito trifase squilibrato: stella con neutro e carichi monofase fra i fili di linea
Tema 5)
Una linea trifase alimenta, alla tensione concatenata di 400V, frequenza 50Hz, i seguenti carichi (fig.1):
- un’impedenza Zs1 formata dalla serie di una resistenza di 20 Ω e una reattanza capacitiva di 30 Ω collegata tra il filo di linea 1 e il neutro;
- un’impedenza Zs2 formata dalla serie di una resistenza di 40 Ω e una reattanza induttiva di 20 Ω collegata tra il filo di linea 2 e il neutro;
- un’impedenza Zs3 formata da una resistenza di 80 Ω, collegata tra il filo di linea 3 e il neutro;
- un’impedenza Z12=50+j50 collegata fra i fili 1 e 2 della linea ;
- un’impedenza Z23=50+j60 collegata fra i fili 2 e 3 della linea;
- un’impedenza Z31=80-j60 collegata fra i fili 3 e 1 della linea.
(Si osservi come queste ultime impedenze possano anche vedersi collegate a triangolo, ma non è indispensabile questa interpretazione).
Determinare tutte le correnti di fase, quella nel neutro e le correnti di linea.

Figura 1) Circuito trifase squilibrato: carico a stella e carichi monofase fra i fili di linea.
SOLUZIONE con il metodo vettoriale.
Si rappresentano i vettori di tutte le tensioni agenti sui carichi del circuito: si tratta delle tre tensioni stellate (espresse dapprima come numeri complessi in forma esponenziale) e delle tre tensioni concatenate, che sono quelle agenti sulle fasi utilizzatrici collegate fra i fili di linea.
Nella rappresentazione degli argomenti si devono effettuare le trasformazioni da radianti a gradi, per agevolare la rappresentazione dei vettori sul diagramma.
Si ricordi sempre qual è la d.d.p. che agisce ai capi delle singole fasi utilizzatrici e la si rappresenti vettorialmente, tenendo conto della posizione nel piano di Gauss.
I moduli di tutte le grandezze si intendano, naturalmente, espressi nel S.I.

Figura 2) Diagramma delle tensioni stellate e concatenate nel piano di Gauss
Calcolo delle correnti di fase del carico a stella:

Calcolo delle correnti assorbite dai carichi collegati fra i fili di linea, in modulo e argomento:

Applicando il primo principio di Kirchhoff ai nodi (tutti i punti equipotenziali formano un solo nodo) si valutano le correnti di linea e del neutro. Per comodità tutte le correnti di linea e del neutro sono state dirette dal generatore al carico.
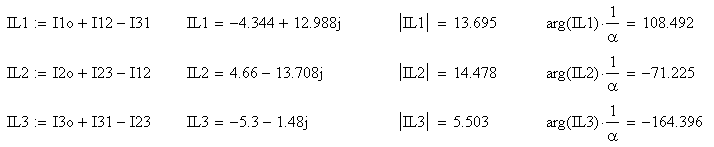
![]()
Come verifica si esegue la seguente somma vettoriale, che dà come risultato un valore nullo, come deve essere:
![]()
Le correnti sono rappresentate nei due diagrammi seguenti.
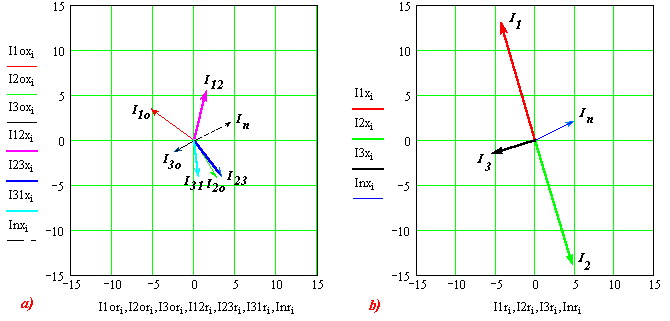
Figura 3) Correnti di fase e nel neutro in
a); correnti di linea e nel neutro b).Si verifichino le posizioni dei vettori dai valori espressi sopra: sia dall’espressione simbolica, sia controllando gli sfasamenti riferiti all’asse reale positivo. I diagrammi sono stati rappresentati separatamente, per tentarne una migliore comprensione, ma occorre esercitarsi a ripeterli con scale più ampie, verificando inoltre le relazioni vettoriali dedotte dal principio di Kirchhoff e scritte sopra.
Le operazioni di calcolo dedotte con Mathcad (www.mathcad.com) (http://www.gmsl.it/mathcad/index.html) vanno naturalmente interpretate come relazioni fra vettori.
![]()
10_Circuito trifase equilibrato: stella con neutro e carico a triangolo
Si esamina la soluzione di un tema simile al precedente, ma con i carichi equilibrati: uno a stella e uno a triangolo, secondo lo schema di fig.4.
Per la soluzione, pur essendo i carichi equilibrati, non è sufficiente calcolare i moduli delle correnti, perché, quando si devono calcolare le correnti di linea, occorrerebbe rifarsi comunque al calcolo vettoriale.
La via risolutiva più semplice consiste nell’applicare il teorema di Boucherot, già citato, da sostituire alla somma di vettori col metodo simbolico.
In realtà si tiene conto del fatto che le correnti sono tra loro sfasate, ma se ne nasconde il procedimento passando attraverso la valutazione della potenze apparenti. Anche le potenze apparenti, in realtà si sommano vettorialmente, ma senza ricorrere ai numeri complessi. In effetti basta sostituire ai vari carichi un unico carico trifase equilibrato: la sua potenza apparente, che è quella di tutto l’impianto, consente di determinare le correnti di linea.
Vediamo come.

Figura 4) Carichi equilibrati su linea trifase con neutro.
Tema 6)
Una linea trifase alimenta, alla tensione concatenata di 400V, frequenza 50Hz, i seguenti carichi trifase equilibrati (fig.4):
- un carico trifase a stella collegato fra i fili di linea e il neutro, di cui ogni impedenza vale Zs=20-j30;
- un carico trifase a triangolo, posto fra i fili di linea, di cui ogni impedenza vale ZD=50+j50.
Determinare tutte le correnti di fase e le correnti di linea.
Soluzione
Se si adottasse il procedimento vettoriale, si determinerebbero le correnti come in fig.5. Per non creare confusione è sottintesa la rappresentazione delle terne delle tensioni, per le quali si ripete identicamente la fig.2.
La determinazione della corrente di linea sarebbe possibile eseguendo ad esempio la seguente somma di vettori, in base al I Principio di Kirchhoff al nodo1:
![]()
come si può verificare dal diagramma di fig.5.
Le altre correnti di linea saranno uguali in modulo e sfasate fra loro di 120°, essendo equilibrato anche il circuito equivalente complessivo, "visto" dal generatore.
La corrente nel neutro è nulla, provenendo dalla somma vettoriale delle correnti a 120° del carico a stella.
Non si addice alla semplicità questa proposta di soluzione. E’ più semplice e rapida l’applicazione del teorema delle potenze di Boucherot.
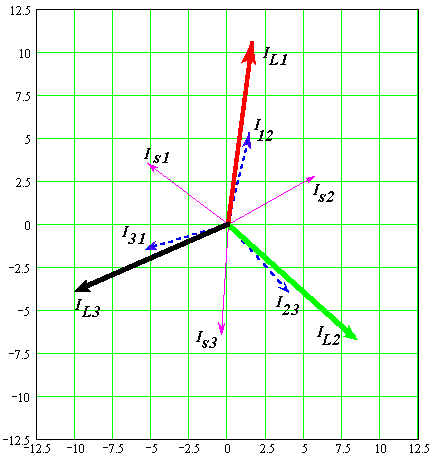
Figura 5) Diagramma nel piano di Gauss delle correnti di fase e di linea del Tema 6.
1) Si determinano le correnti di fase, l’angolo di sfasamento, il f.d.p. e le potenze del carico a stella.
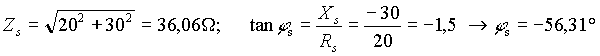
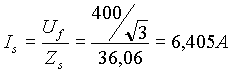
![]()
oppure
![]()
Per la potenza reattiva della stella, tenendo conto del segno (Zs è di tipo R-C !):
![]()
2) Si determinano le correnti di fase, l’angolo di sfasamento, il f.d.p. e le potenze del carico a triangolo equilibrato.
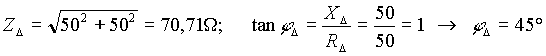
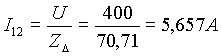
La potenza attiva del carico a triangolo vale
![]()
La potenza reattiva è
![]()
oppure
![]()
Si riducono i due carichi a un solo carico equivalente, che si può ritenere collegato a stella (v. § 1)
In questo consiste il teorema delle potenze e pertanto si calcolano:
·
la potenza attiva totale sommando le potenze attive dei due carichi di fig.4;·
la potenza reattiva totale sommando algebricamente le potenze reattive dei due carichi;·
la potenza apparente totale dalla somma vettoriale delle potenze apparenti dei due carichi (v. §12 e §16-1); in effetti si preferisce determinare il modulo della potenza apparente totale più semplicemente dal triangolo delle potenze, essendo la potenza apparente l’ipotenusa del triangolo rettangolo i cui cateti sono la potenza reale e la potenza reattiva.
Quindi la potenza attiva e reattiva dell’impianto sono
![]()
![]()
Infine la potenza apparente totale è
![]()
e da questo valore si determina la corrente totale della linea di alimentazione, tenendo presente che
![]()
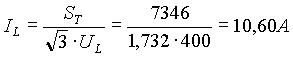
Essendo il carico a stella di tipo equilibrato non vi sarà corrente nel neutro per cui, in questo caso, la sua presenza è ininfluente sul funzionamento del circuito esistente in fig.4.
Il fattore di potenza dell’intero carico, quello che "vede" il fornitore di energia elettrica, si calcola ad esempio con l’espressione
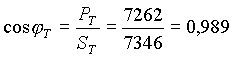
![]()
11_Motore trifase e carichi monofase
Tema 7)
Una linea trifase con neutro alimenta, alla tensione concatenata di 400V i seguenti carichi:
- un motore asincrono trifase di potenza resa Pr = 5 kW, rendimento h =0,850, fattore di potenza cosj m=0,820;
- un carico monofase puramente resistivo, collegato fra il filo di linea 2 e il neutro: Z20=50+j0;
- un carico monofase collegato fra i fili di linea 3 e 1: Z31=40+j40
Si calcolino
1) le correnti di linea e nel filo neutro.
2) Il fattore di potenza convenzionale dell’impianto.
Figura 6) Schema dell’alimentazione dei carichi del Tema 7.
Soluzione
1) Si stabiliscono i versi delle correnti nel circuito, come in fig.6.
Il motore trifase è un carico equilibrato.
Se non è noto il tipo di collegamento delle tre fasi interne, si ritiene sempre, per comodità, che il carico sia a stella equivalente. Pertanto gli sfasamenti che ora si determinano, vanno riferiti alle tensioni stellate.
Dai dati del motore si deve calcolare la potenza assorbita e da questa si determina la corrente di linea che la macchina preleva dalla rete.

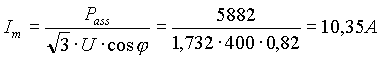
Lo squilibrio complessivo dell’utenza impone la rappresentazione con il metodo simbolico delle singole correnti.
Le correnti assorbite dal motore sono sfasate dell’angolo j m in ritardo rispetto alle tensioni stellate:
cosj m → j m = 34,92°
![]()
e sostituendo i valori noti si ottengono
Si calcolano le due correnti dei carichi monofase, mettendo in gioco solo le tensioni interessate alla produzione delle correnti stesse: la tensione stellata U20 e quella concatenata U31:
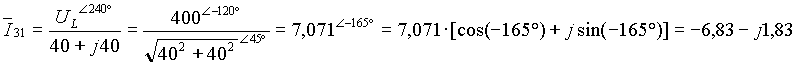
Dall’applicazione del primo principio di Kirchhoff ai nodi dello schema si calcolano, vettorialmente, le correnti di linea.
Sostituendo i valori calcolati sopra si ottengono
I moduli e gli argomenti (rispetto all’asse reale) si deducono dai seguenti valori finali:
Come verifica si può controllare che, nei limiti delle approssimazioni apportate, si ha:
Le correnti sono disegnate in fig. 7, sfasate rispetto alle tensioni, rappresentate anch’esse, ma in scala diversa, non riportata in figura.
Figura 7) Diagramma del Tema 7. I valori numerici sono riferiti alle sole correnti.
2) Si calcolano le potenze dell’impianto, applicando il teorema di Boucherot.
Potenze del motore trifase riferite all’ingresso del motore stesso:
Potenze del carico monofase, posto fra il filo 1 e il neutro (è una resistenza pura, il fattore di potenza è unitario e la potenza reattiva è nulla):
Potenze del carico monofase, posto fra il filo 1 e il filo 3:
Potenza attiva e reattiva totali:
Potenza apparente totale e fattore di potenza convenzionale (essendo squilibrato il carico totale):
prof. Attilio Barra e-mail: elettrotecnica@barrascarpetta.org
prof. Antonio Scarpetta e-mail: laboratorio@barrascarpetta.org
Indice generale Elettro home
map Indice moduli Indice modulo 2