Indice
generale
Elettro
home
![]() map
Indice moduli
Indice
modulo 3
map
Indice moduli
Indice
modulo 3
M o d u l o 3
S i s t e m i T R I F A S E
RISOLUZIONE DI RETI TRIFASE
Le grandezze di fase si indicheranno col pedice f (ad esempio Ef, Uf, If);
le tensioni o le correnti di linea potranno avere il pedice L (ad esempio EL, UL, IL); .
le grandezze di linea, per comodità, verranno spesso scritte senza il pedice.
Quando si forniscono i dati di un problema, non specificando alcunché, si intendono quelli di linea. Le grandezze di linea si possono misurare più facilmente delle grandezze di fase: si misurano infatti la tensione fra due fili della linea di alimentazione e le correnti che percorrono i fili della linea stessa.
Per la risoluzione dei circuiti trifase si applicano i procedimenti già noti per la risoluzione dei circuiti monofase in corrente alternata.
Occorre però ricordare che le cose si complicano quando il carico trifase è squilibrato. Poiché le tensioni di fase, e cioè quelle che agiscono su ogni singola fase, occupano una ben precisa posizione nel piano di Gauss, occorre sempre impostare la risoluzione tenendo conto di questa importante osservazione e quindi è necessario ricorrere alla notazione complessa, ovvero al metodo simbolico.
Minori difficoltà si presentano invece nella risoluzione di carichi equilibrati. Per essi spesso è sufficiente usare i moduli delle tensioni e delle correnti o il teorema di Boucherot delle potenze.
4_Rappresentazione vettoriale delle terne di tensioni simmetriche.
Si abbia una linea trifase con tensione concatenata di 400V.
Si rappresentino le terne, con senso ciclico diretto, mediante vettori e in forma complessa.
Con riferimento alla fig. 1) si possono scrivere le seguenti relazioni, ricordando anche che il verso convenzionale positivo degli angoli è quello antiorario, partendo dall’asse reale positivo:
![]()
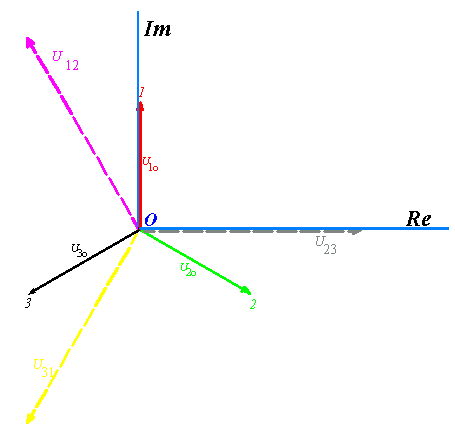
Figura 1) Piano di Gauss per la rappresentazione vettoriale delle tensioni di fase e concatenate.
![]()
I vettori sono stati espressi in forma polare o di Steinmetz (metodo americano o esponenziale abbreviato).
La seguente rappresentazione è fatta con numeri complessi in forma trigonometrica e poi in forma binomia o rettangolare.
![]()
![]()
![]()
Si ricordi allora di rappresentare un vettore a seconda del quadrante in cui si trova. In notazione trigonometrica simbolica si esegue l’operazione
![]()
![]()
è il modulo del vettore in esame (generalmente è il valore efficace);
In modo analogo si procede per le tensioni concatenate, di modulo 400 V e tenendo sempre in considerazione la posizione nel piano di Gauss.
![]()
![]()
![]()
5_Carico trifase squilibrato, collegamento a stella con neutro.
Negli schemi seguenti non verrà più disegnata la terna delle fasi generatrici, che si sottintende simmetrica e diretta (R-S-T oppure 1-2-3: la fase 2 succede alla fase 1 con 120° di ritardo; la fase 3 a sua volta ritarda di 120° rispetto alla 2 o anticipa di 120° rispetto alla 1).
L’inversione di una di queste fasi porta al senso ciclico inverso, in cui la successione dei ritardi è R-T-S oppure 1-3-2. Questa diversa situazione deve essere precisata, altrimenti si intenderà fare riferimento alle terne con senso ciclico diretto.
Per conoscere la successione ciclica delle fasi esiste il sequenscopio (di tipo statico, schematizzato nel Tema L7, o di tipo rotante). Noto il senso ciclico delle fasi si può ad esempio stabilire con certezza il senso di rotazione che avrà un motore trifase a campo rotante all’atto dell’alimentazione.
Lo scopo dei seguenti temi risolti è quello di fornire una panoramica sui casi tipici di impostazione e risoluzione.
Tema 1)
Una linea trifase con neutro alimenta, alla tensione concatenata di 400V, f=50Hz, tre impedenze collegate a stella come in figura, di valore
![]()
Determinare:
1) le correnti di linea e del neutro, vettorialmente e in modulo;
2) calcolare vettorialmente le tensioni concatenate;
3) rappresentare il diagramma tensioni-correnti.
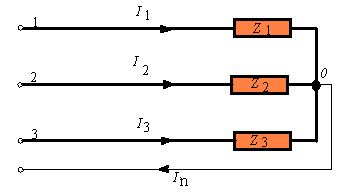
Figura 1) Carico trifase a stella con centro stella collegato al neutro.
una corrente di fase è data dal rapporto fra la tensione di fase che la produce (intesa come vettore che si trova in una ben precisa posizione nel piano di Gauss) e l’impedenza della fase espressa sempre in forma vettoriale.

Figura 2) Tensioni e correnti nel piano di Gauss
Figura 3) Diagramma vettoriale tensioni di fase-correnti di fase. Per la risoluzione si poteva anche seguire il metodo grafico , ma con qualche approssimazione da mettere in conto, specie nel calcolo di In .
Come verifica, dal diagramma si possono fare le seguenti osservazioni:
6_Carico trifase equilibrato, collegamento a stella con neutro.
Lo stesso tipo di collegamento viene ora risolto nel caso in cui il carico sia costituito da una stella equilibrata.
Si confrontino successivamente le due diverse impostazioni.
Tema 2)
Una linea trifase con neutro alimenta, alla tensione concatenata di 400V, f=50Hz, tre impedenze collegate a stella come in figura 1, di valore
![]()
1) le correnti di linea e del neutro, vettorialmente e in modulo;
2) rappresentare il diagramma tensioni-correnti.
Soluzione 1)

Figura 4) Terna simmetrica delle tensioni di fase e terna equilibrata delle correnti del carico equilibrato.
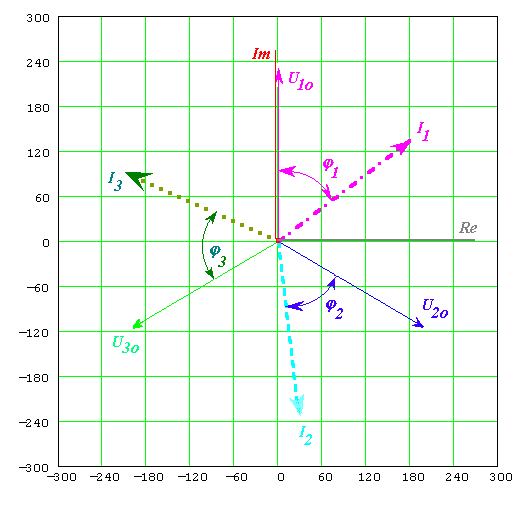
Figura 5) Diagramma U-I del carico trifase equilibrato: sono identici i moduli delle correnti e gli sfasamenti del carico.
Soluzione 2) (consigliata)
Solo per carichi equilibrati, come in questa applicazione, si può procedere alla determinazione del modulo di una corrente di fase, essendo le altre identiche in modulo:
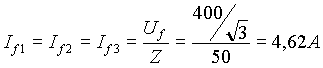
Le tre correnti sono sfasate di 53,13° rispetto alle proprie tensioni di fase e fra loro l’angolo è di 120°.
Come importante conseguenza si evidenzia il fatto che nel filo neutro la somma vettoriale delle tre correnti risulta nulla, come si vede anche facilmente dalla posizione delle tre correnti di fase nel diagramma.
L’assenza di corrente nel filo neutro è una caratteristica del carico equilibrato, a differenza di ciò che si è constatato nell’esempio precedente (la corrente In era addirittura di modulo superiore a quelle della linea).
Questa situazione giustifica il fatto che il filo neutro si potrebbe addirittura eliminare: i potenziali del centro stella del generatore (non rappresentato in questo schema) e del centro stella del carico coincidono anche se manca il neutro (non è invece così se il carico è squilibrato e il neutro non esiste, ma si vedrà al §12).
Si insiste sul fatto che la corrente è nulla nel neutro solo per carichi trifase equilibrati. Quindi, in questo caso, il carico trifase può funzionare correttamente sia con la presenza del neutro, sia in sua assenza (linea trifase a tre fili senza neutro).
Tanto minore è lo squilibrio, tanto minore è la corrente che percorre il neutro. Nel tema precedente lo squilibrio era elevato, specie per la diversità dei singoli sfasamenti.
La notevole semplificazione del procedimento appena discusso, si ribadisce ancora valida per carichi equilibrati, risparmia tutto il complesso procedimento seguito per il tema n°1.
prof. Attilio Barra e-mail: elettrotecnica@barrascarpetta.org
prof. Antonio Scarpetta e-mail: laboratorio@barrascarpetta.org
Indice
generale
Elettro
home
![]() map
Indice moduli
Indice
modulo 2
map
Indice moduli
Indice
modulo 2
<<<== <= U n i t à up => ==>>>