Indice generale Home Indice moduli
Correnti
alternate – Sistemi MONOFASE
![]()
12_Risoluzione di circuiti in serie – Impedenza
totale
Per la risoluzione di carichi collegati in serie, cioè percorsi dalla stessa corrente, si determina l’impedenza totale. Occorre ricordare ancora che i diversi sfasamenti delle impedenze, e di conseguenza delle singole cadute di tensione ai capi, impongono che la loro somma sia vettoriale e non una semplice somma numerica dei singoli moduli.
La
somma vettoriale si riferisce sia al calcolo dell’impedenza totale, sia al
calcolo della tensione totale, note le singole c.d.t. vettoriali.
Nel seguito si applicherà il teorema di Kennelly-Steimetz:
per la
risoluzione dei circuiti in regime sinusoidale le relazioni sono analoghe a
quelle adottate per le reti in corrente continua, purché alle grandezze scalari
si sostituiscano le grandezze vettoriali, alle resistenze si
sostituiscano le impedenze e alle conduttanze le ammettenze
(v. dopo). Le operazioni si eseguono, ad esempio, con i numeri complessi.
Si risolve un esempio numerico riferito a due impedenze in serie.
Esempio 1) Il circuito di fig.1a), percorso dalla corrente di 10A in valore efficace, è costituito dalla serie di due impedenze così espresse:
![]()
![]()
Calcolare
- le cadute di tensione prodotte dalle due impedenze,
- la tensione UAC fornita dal generatore, posto tra i punti A-C,
- l’impedenza totale ZT,
- lo sfasamento totale;
- tracciare il diagramma delle cadute di tensione e il triangolo dell’impedenza totale.
_____________________
Calcolo dell’impedenza totale
![]()
essendo
![]()
![]()
![]()
I moduli delle impedenze e i relativi sfasamenti sono i seguenti:
![]()
![]()
![]()
Calcolo vettoriale delle cadute di tensione:
![]()
![]()
La tensione totale fra i punti A-C, espressa mediante le relazioni
![]()
vale
![]()
Si riassumono le grandezze, scrivendole in forma esponenziale:
![]()
![]()
![]()
![]()
![]()
Per tracciare il diagramma corrente-tensioni di fig. 1c) è opportuno collocare sull’asse reale la grandezza nota e comune alle due impedenze in serie, che è, in questo esercizio, la corrente.
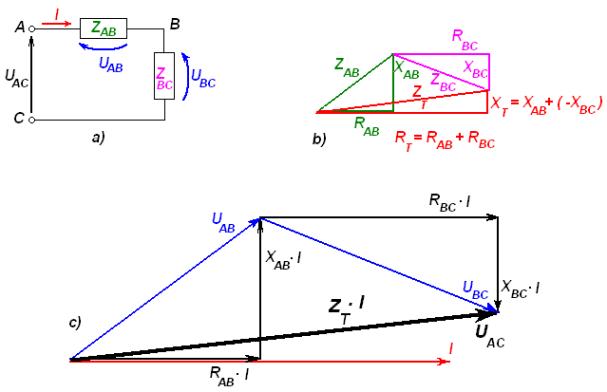
Figura 1a) Impedenze in serie; b) triangolo delle impedenze; c) diagramma corrente-tensioni
13_Risoluzione di circuiti in parallelo – Metodo
delle conduttanze, suscettanze, ammettenze - Impedenza equivalente
Mentre in serie si determina la impedenza totale sommando vettorialmente le singole impedenze,
nei rami in parallelo
si sommano vettorialmente le singole ammettenze,
per ottenere quella totale.
L’ammettenza viene definita come il reciproco dell’impedenza.
Partendo per ipotesi da una impedenza di tipo ohmico-induttivo e utilizzando il metodo simbolico si ottiene:
![]()
essendo la conduttanza, parte reale espressa in ‘siemens’:
![]()
e la suscettanza, anch’essa espressa in ‘siemens’ come anche l’ammettenza:
![]()
Si noti, perché ciò sarà utile per la convenzione dei segni sul tipo di carico, che l’impedenza e l’ammettenza corrispondente differiscono per il segno del cateto, come si nota in fig.2) per il carico R-L. Per carichi R-C si scambiano ovviamente le considerazioni.

Figura 2) Differenza fra i segni della parte reattiva nei triangoli dell’impedenza e dell’ammettenza per un carico R-L . Per un carico R-C serie si scambiano i segni in modo duale.
· Per due rami in parallelo si può sempre calcolare l’impedenza equivalente come si faceva, in genere, per le resistenze in parallelo, ma ricordando che qui vale il teorema citato di Kennelly-Steimetz, e quindi vettorialmente:
![]()
· In generale, con riferimento a tre rami in parallelo (fig.3a), si opera ad esempio con le seguenti relazioni
![]()
ed essendo per definizione
![]()
l’ammettenza totale diventa
![]()
Essa equivale ai rami in parallelo e, alimentata alla stessa tensione, assorbe la stessa corrente totale erogata dal generatore (figg. 3a-b)
Per ritornare alla rappresentazione della impedenza equivalente, inversamente si ottiene
![]()
Per quanto riguarda le correnti, essendo i rami in parallelo sottoposti alla stessa tensione, si applica il primo principio di Kirchhoff :
![]()
ed ancora
![]()
![]()
Il modulo della corrente totale è deducibile dal seguente
calcolo:
![]()

Figura 3a) Tre rami in parallelo e circuito equivalente; b) conduttanze e suscettanze dei rami ed ammettenza totale; c) diagramma vettoriale con valori numerici dell’esempio 2 (il ramo 2 è di tipo R-C).
_______________
Esempio 2) Il circuito di fig.3a), formato da tre rami in
parallelo (e dunque sottoposti alla stessa tensione),
presenta i seguenti
valori noti:
![]()
![]()
![]()
Il generatore alimenta il circuito con tensione sinusoidale, il cui valore efficace è di 500V, alla frequenza f di 50Hz .
Calcolare il circuito equivalente serie, la corrente erogata totale e lo sfasamento complessivo.
_______________
Calcolo delle singole reattanze:
X1
= XL1
= ω · L1 = 2πf · L1
= 314 · 150 · 10-3 = 47,12
Ω
![]()
Risoluzione con i moduli delle conduttanze, suscettanze e ammettenze
1) Calcolo delle conduttanze di ogni ramo:
![]()
![]()
![]()
2) Calcolo le suscettanze di ogni ramo (il segno è opposto a quello convenzionale delle reattanze: negativo per le suscettanze induttive e positivo per le suscettanze capacitive):
![]()
![]()
![]()
3) Calcolo della conduttanza totale (somma numerica) e della suscettanze totale (somma algebrica):
![]()
![]()
4) Calcolo dell’ammettenza totale, dedotta con il teorema di Pitagora dal triangolo dell’ammettenza totale (le ammettenze si sommano vettorialmente, tenendo conto quindi degli sfasamenti singoli, ma qui è sufficiente calcolarne il modulo):
![]()
5) Calcolo dei parametri equivalenti-serie in base alle relazioni (7) (si ricordino le vicende del segno: sono positive la XL e la BC; sono negative la XC e la BL):
![]()
Il circuito di partenza di fig.3a è dunque equivalente ad una impedenza formata dalla serie di una resistenza Re=34,37Ω e di una reattanza induttiva Xe=9,846Ω
6) Calcolo del modulo della corrente totale
![]()
Lo sfasamento complessivo del circuito si può ricavare o dal triangolo dell’ammettenza totale o dal triangolo dell’impedenza equivalente serie:
![]()
Per determinare le componenti delle correnti in fase con la tensione (IG) e quelle a 90° (IB), dalle relazioni (9) si ottiene, ad esempio per la corrente totale:
![]()
come si può verificare dal diagramma di fig.3c)
Procedimento con metodo simbolico.
Anziché con i moduli si poteva procedere con il metodo simbolico, mediante l’applicazione delle relazioni 6) , 7) , 8) e 9) ottenendo così:
![]()
![]()
![]()
![]()
con correnti nei rami e totale (la tensione, grandezza comune ai tre rami, si pone sull’asse reale):
![]()
![]()
![]()
![]()
La fig.3c) riproduce, in scala,
i risultati ottenuti, evidenziando il comportamento induttivo dei rami 1 e 3 e
quello capacitivo (corrente in anticipo sulla tensione) del 2° ramo. La
corrente totale, in ritardo sulla tensione, conferma che il circuito, nel suo
insieme, è un carico ohmico-induttivo.
· Anziché usare il procedimento descritto si può calcolare, ad esempio, l’impedenza equivalente prima fra i rami 1 e 2 (relazione a) e successivamente porre il risultato in parallelo col ramo 3, ottenendo
![]()
_______________
Esempio 3) Data un’impedenza, serie tra una resistenza R=8Ω e una reattanza induttiva X=6Ω, si determinino i parametri del bipolo equivalente parallelo, cioè tale che, alimentato dalla stessa tensione, assorba la stessa corrente e conservi lo stesso sfasamento complessivo.

Figura 4) Equivalenza tra circuito serie e circuito parallelo.
Si valutano i parametri equivalenti:
![]()
a cui corrispondono, in ohm, i valori dei due rami in parallelo di fig.4):
![]()
![]()
prof. Attilio Barra e-mail: elettrotecnica@barrascarpetta.org
prof. Antonio Scarpetta e-mail: laboratorio@barrascarpetta.org
Indice generale Home Indice moduli