Indice generale      Elettro home      map      Indice moduli      Indice modulo 4

 M o d u l o  4

T r a s f o r m a t o r e

<<==    <=        U n i t à   13        =>    ==>>

§13)  Parallelo dei trasformatori

Quando il carico richiede una potenza superiore a quella nominale delle macchine in funzione occorre inserire in parallelo un aiuto di potenza, da parte di uno o più trasformatori aggiuntivi.

Il collegamento viene detto in parallelo quando i primari sono allacciati alla stessa linea di alimentazione e gli avvolgimenti secondari risultano anch’essi collegati sulle stesse sbarre di uscita, cui fa capo il carico complessivo.

Nelle applicazioni successive, per semplicità, si discute il funzionamento in parallelo di due sole macchine, ma il procedimento è valido per qualunque numero di trasformatori.

Fig. 17) Schema unifilare di due trasformatori in parallelo.

Condizioni ideali di parallelo

1.      I due trasformatori hanno identico rapporto di trasformazione a vuoto e stessa tensione nominale primaria.

 Conseguenza: non vi è corrente di circolazione tra le due macchine  a vuoto.

2.      Si collegano alla linea dei secondari i morsetti corrispondenti delle due macchine: si dicono corrispondenti due morsetti secondari con uguale polarità, ossia quando i loro potenziali sono in ogni istante uguali, contemporaneamente maggiori o contemporaneamente minori. Nelle applicazioni trifase i morsetti d’uscita devono dar luogo alla stessa successione ciclica delle fasi e le due terne di tensioni devono coincidere (ciò è garantito anche dal punto 3). In tal modo in ogni maglia agiscono due f.e.m. in opposizione di fase.

3.      I trasformatori trifase in parallelo devono appartenere allo stesso gruppo.

Normalmente i gruppi sono rappresentati dai numeri 0-6-5-11 ai quali corrispondono gli sfasamenti tra la terna delle f.e.m. del lato b.t. rispetto alla terna delle corrispondenti f.e.m. del lato A.T. divisi per 30. Tale sfasamento, detto spostamento angolare fra le due terne di tensioni, vale rispettivamente 0°, 180°, 150°, 330°  (p.e.  Yd11  significa collegamento Y-d con indice di gruppo 11 e conseguente spostamento angolare di 330°).

Per trasformatori in parallelo appartenenti allo stesso gruppo e identici rapporti di trasformazione  non vi sono differenze vettoriali fra le tensioni di ogni singola maglia del secondario, essendo le due terne coincidenti e in opposizione di fase: non vi è dunque alcuna corrente di circolazione (v. fig. 18).

Se invece cambiano i sensi di avvolgimento delle bobine, o se si scambiano i morsetti di ingresso con quelli di uscita di un avvolgimento, o se i collegamenti degli avvolgimenti sono diversi (uno p.e. con collegamento Y-y e l’altro con collegamento Y-d, ecc.) si producono delle correnti di circolazione che possono danneggiare i trasformatori, addirittura già nel funzionamento a vuoto: le due terne delle tensioni secondarie non potendosi sovrapporre danno differenze di tensione nelle singole maglie ed  elevate correnti.

4.      I trasformatori hanno la stessa U_cc%. Solamente in tal caso la corrente totale del carico si suddivide fra i due trasformatori in proporzione alle rispettive potenze nominali:

In altre parole, se le tensioni di c°.c°. sono diverse, si carica di più il trasformatore avente minore c.d.t. interna (determinata nel funzionamento singolo). Per chiarezza si vedano gli esempi numerici seguenti.

5.      Se si verifica anche l’uguaglianza degli sfasamenti caratteristici  allora le singole correnti secondarie, risultando in fase fra loro, contribuiranno alla corrente totale secondaria con il valore minimo. I triangoli delle impedenze equivalenti devono pertanto essere simili (sono uguali solo per trasformatori gemelli).

Esempi di determinazione del gruppo di un trasformatore

Esempio di parallelo con dati che non soddisfano tutte le condizioni del parallelo ideale  

E’ questo uno dei casi più completi, ma piuttosto laborioso per la soluzione.

I due trasformatori di figura 17) e 18), A e B, allacciati alle sbarre primarie alla tensione concatenata di 12 kV e frequenza 50 Hz, alimentano un carico collegato a stella avente f.d.p. unitario (carico resistivo puro) e resistenza per ogni fase utilizzatrice di 3 Ω .

I dati noti sono i seguenti:

Si determinino:

·        la corrente di circolazione a vuoto;

·        la tensione e la corrente del carico;

·        le correnti erogate dai due trasformatori.

SOLUZIONE

I due trasformatori non soddisfano le condizioni ideali 1, 4, 5 citate sopra.

I collegamenti interni sono tutti a stella (in caso diverso occorrerebbe riferirsi sempre al collegamento equivalente Y/y).

Nel procedimento che segue si calcolano le correnti nominali e i parametri equivalenti riportati al secondario, per poi determinare la tensione al carico, le correnti secondarie effettivamente disponibili e infine discutere le condizioni di funzionamento.

Per il calcolo della corrente di circolazione  presente nel funzionamento a vuoto con le due macchine collegate alla sbarra primaria e alla sbarra secondaria, con interruttore del carico aperto, si applica il secondo principio di Kirchhoff (v. fig. 19 con interruttore aperto):

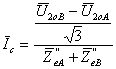
Sostituendo si ricava, dopo l’elaborazione della formula, il seguente valore

(Si osservi che i risultati sono relativi alle tensioni nominali secondarie poste sull’asse reale)

Questo valore di corrente dà luogo, a vuoto, a perdite nel rame di una certa entità. Dal punto di vista pratico è importante che tale corrente non superi il valore più basso delle correnti nominali dei trasformatori 
(qui è I_c < 70,93 A).

Fig. 18)  Schema ‘equivalente’ per lo studio del parallelo di due trasformatori, di cui sono stati riportati i parametri al secondario. I due centri stella dei trasformatori e il centro stella del carico equilibrato hanno lo stesso livello elettrico O e pertanto è come se questi tre nodi fossero collegati fra loro. In colore è rappresentata una maglia nella quale agiscono le f.e.m. di una fase di A e di B riportate al secondario (che in questo problema sono diverse) e in cui gli ostacoli sono dovuti alle singole impedenze di corto circuito anch’esse riportate al secondario.

Si ottiene così la fig. 19) che schematizza il già noto circuito equivalente di una fase di ogni trasformatore, studiato al secondario, con le due macchine in parallelo che alimentano il carico.

Si passa adesso al calcolo della tensione di fase a carico, mediante il corollario di Tank    con la relazione vettoriale

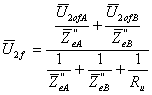
(v. fig. 19 con interruttore chiuso).

La sostituzione dei valori noti porta, sempre in forma laboriosa, ai risultati

Fig. 19) Una fase dell’intero circuito con i parametri riportati al secondario. Quando l’interruttore “t” è aperto si ha il funzionamento a vuoto, ma con i trasformatori aventi i morsetti secondari collegati sulle sbarre d’uscita: si può calcolare la corrente di circolazione a vuoto nella maglia formata dalle due f.e.m. e dalle impedenze equivalenti.

Nel funzionamento a carico, con “t” chiuso, si può applicare il metodo di Millmann per il calcolo della U_2f , oppure il metodo del circuito equivalente di Thévenin (v. fig. 20).

 Calcolo delle correnti erogate al secondario dalle macchine A e B, con riferimento alla fig. 19):

I moduli delle rispettive correnti valgono:

Le percentuali di carico, che evidenziano la percentuale di erogazione rispetto alla propria corrente nominale, sono le seguenti:

Si conclude dunque che il trasformatore B, pur di potenza inferiore, è costretto a lavorare con una percentuale di carico più del doppio rispetto alla condizione di lavoro del trasformatore A, avente potenza doppia.

Questa situazione di funzionamento si verifica poiché sono diverse le U_cc%, ma non viene a crearsi nessuna situazione pericolosa, con i dati esposti. Certo sarebbe meglio se la percentuale di carico fosse identica: la macchina con potenza doppia erogherebbe una corrente doppia rispetto a quella erogata dalla macchina con potenza minore. Qui la macchina B eroga addirittura una corrente superiore a quella erogata dalla macchina A!

Esempio di parallelo con dati che soddisfano tutte le condizioni del parallelo ideale

Due trasformatori, A e B, allacciati alle sbarre primarie alla tensione concatenata di 12 kV e frequenza 50 Hz, alimentano un carico collegato a stella avente f.d.p. unitario (carico resistivo puro) e resistenza per ogni fase utilizzatrice di 3 Ω .

I dati noti sono i seguenti, modificati dal tema precedente:

Si determinino:

·        la corrente di circolazione a vuoto;

·        la tensione e la corrente del carico;

·        le correnti erogate dai due trasformatori.

SOLUZIONE

I due trasformatori soddisfano tutte le condizioni ideali per il parallelo, citate sopra, diversamente dal tema numerico precedente. Sono qui uguali le tensioni secondarie a vuoto, le tensioni di corto circuito e anche gli sfasamenti dell’impedenza caratteristica di corto circuito.

Il procedimento seguito è ancora identico a quello dell’esercizio precedente, ma con le semplificazioni introdotte dalle condizioni per un parallelo perfetto.

La corrente di circolazione è nulla, poiché nella maglia, visualizzata in colore nella fig. 18) e con lo schema di fig. 19) con interruttore aperto, le due f.e.m. sono in opposizione e con stesso modulo.

Pertanto

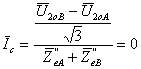
Il calcolo della tensione secondaria a carico, svolto con Millmann (fig. 19 con “t” chiuso), parte dalla relazione

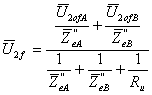
con risultati (non immediati!):

Le correnti erogate ai due secondari risultano pertanto

I moduli delle rispettive correnti valgono:

Le percentuali di carico, che evidenziano la percentuale di erogazione rispetto alla propria corrente nominale, sono le seguenti:

- Diversamente dal tema proposto in precedenza, qui sono rispettate le condizioni di parallelo ideale e quindi:

·        L’uguaglianza delle tensioni nominali secondarie non dà luogo a corrente di circolazione.

·        L’uguaglianza delle tensioni U_cc%  impone l’erogazione di corrente proporzionale alle proprie potenze nominali: infatti qui la macchina con potenza doppia  eroga anche una corrente doppia e quindi le percentuali di carico sono identiche: chi più ha più dà.

·        L’uguaglianza degli sfasamenti interni φ_cc porta come conseguenza che le correnti erogate siano in fase: pertanto la corrente erogata al carico proviene dalla somma numerica delle correnti I_2A e I_2B in modulo, le quali sono quindi minime. Se gli sfasamenti interni fossero diversi il trasformatore ‘A’ erogherebbe una corrente superiore a 51,03A e ‘B’ erogherebbe una corrente superiore a 25,51A: per ottenere la corrente di carico di 76,54 A si dovrebbe eseguire la somma vettoriale di due correnti sfasate. Le perdite interne per effetto Joule aumenterebbero e si abbasserebbe il rendimento.

       - CASI PARTICOLARI DI FUNZIONAMENTO IN PARALLELO -

Fig. 20) Il circuito a) (fig. 19) viene studiato e risolto con Thévenin (fig. b), mediante il generatore equivalente U_2Th e l’impedenza equivalente di Thévenin Z_Th. Il metodo di risoluzione può essere alternativo a Millmann, seguito in precedenza. La Z_Th sostituisce il parallelo fra Z”_eA e Z”_eB .

1) Si consideri il caso in cui due trasformatori abbiano le stesse tensioni nominali secondarie, ma diversi φ_cc e U_cc .

Risolvendo con Thévenin il circuito di fig. 19) si ottiene lo schema di fig. 20-b).

Si ricorda che per determinare la corrente nel carico Z_u e la tensione ai suoi capi con Thévenin, si immagina di effettuare un taglio ai capi della Z_u , tra i punti R e 0 della figura 20-a). Allo schema che rimane a sinistra del taglio si sostituisce quello equivalente b) in cui

·         la tensione del generatore U_2Th è quella che si “vede” ai capi del taglio R0 senza la  Z_u . Qui, essendo uguali U_2oA e U_2oB anche la tensione di Thévenin  ha lo stesso valore, cioè

U_2Th = U_2ofA = U_2ofB

·         L’impedenza equivalente Z_Th è quella vista sempre ai capi del taglio quando i generatori di tensione dello schema rimasto sono cortocircuitati. Pertanto rimangono le impedenze Z”_eA e Z”_eB in parallelo, come rappresentato nella fig. 20).

A questo punto si rimette l’impedenza tagliata e si risolve il semplice schema equivalente di fig. 20-b) , dove la Z_Th sostituisce il parallelo fra Z”_eA e Z”_eB .

Si calcola quindi, con metodo simbolico:

Conseguentemente la corrente e la tensione richieste sono date dalle relazioni

2) Si consideri il caso in cui due trasformatori abbiano le stesse tensioni nominali secondarie e gli stessi φ_cc .

Si semplifica un po’ il calcolo richiesto dalla (1) per determinare l’impedenza equivalente di Thévenin, con la relazione facilmente verificabile

in cui compaiono solo i moduli delle impedenze di corto circuito. Naturalmente le correnti erogate al secondario da ogni macchina saranno in fase fra loro e la corrente al carico sarà la loro somma numerica.

3) Si consideri il caso molto particolare, ma non raro nelle applicazioni, in cui due trasformatori siano “gemelli”, ovvero con i seguenti dati identici

e appartenenti naturalmente allo stesso gruppo.

La (1) si semplifica ulteriormente e si pone semplicemente

La tensione al carico può anche calcolarsi ricorrendo alla c.d.t. industriale.

Infatti, essendo per la (26-§7) applicata al trifase

si ricava la tensione concatenata U₂, noti la corrente del carico e il suo sfasamento:

prof. Attilio Barra e-mail: elettrotecnica@barrascarpetta.org

prof. Antonio Scarpetta e-mail:  laboratorio@barrascarpetta.org

 Indice generale      Elettro home      map      Indice moduli      Indice modulo 4

<<==    <=        Unità    up        =>    ==>>