Indice generale      Elettro home      map      Indice moduli      Indice modulo 4

 M o d u l o  4

T r a s f o r m a t o r e

<<==    <=        U n i t à   4        =>    ==>>

§4)  Il trasformatore a carico

Il primario sia alimentato alla tensione di rete avente valore efficace costante U₁. Se ai morsetti del secondario è collegato un carico la f.e.m. secondaria E₂ genera la circolazione della corrente secondaria I₂ sia nel carico stesso, sia nelle spire N₂, con conseguente f.m.m. N₂I₂.

Poiché è costante la tensione U₁ e, come si è già visto, potendosi ritenere trascurabili le c.d.t. dovute alla resistenza dell’avvolgimento primario e della reattanza che tiene conto dei flussi dispersi primari, ne consegue che si possa confondere la U₁ con la E₁. Quindi anche la f.e.m. E₁, responsabile del rigido legame col flusso, non potrà modificarsi e quindi nemmeno il flusso utile, che rimarrà, o potrà ritenersi con ottima approssimazione, costante in qualunque condizione di funzionamento, in particolare sia con trasformatore a vuoto, sia con trasformatore a carico, purché non si modifichino la tensione e la frequenza di rete.

Ovviamente, con flusso costante, anche le amperspire risultanti non potranno modificarsi nel passaggio da vuoto a una condizione di funzionamento a carico.

Deve quindi, per reazione (e per il principio di conservazione dell’energia), prodursi al primario una f.m.m. uguale e contraria a quella richiamata dalla corrente di carico I₂:

Il trasformatore richiede pertanto al generatore della rete di alimentazione la corrente di reazione I’₁ la quale, percorrendo la parte ideale del trasformatore, si somma alla corrente I_o , che a vuoto era l’unica corrente esistente nel trasformatore. Dalla rete dunque il trasformatore a carico richiede la corrente totale primaria

Per le f.m.m. valgono le espressioni:

Fig. 6) Correnti e f.m.m. nel trasformatore a carico.

Per maggior rigore si potrebbe notare che al variare della corrente assorbita variano le c.d.t. per cui, a parità di U₁, la E₁, che lega rigidamente il flusso con la (7), cambia modulo. Per le applicazioni numeriche pratiche, come si è notato più volte, queste c.d.t. si ritengono esigue e quindi, ponendo U₁ E₁ si può studiare la macchina come se funzionasse sempre a flusso costante, a vuoto e con qualunque carico al secondario.

§ 4 a)  Equazioni e diagramma del trasformatore a carico

- Rapporto spire e rapporto di trasformazione a vuoto

Dalla prima delle (14) si ricava, in modulo

  Tenendo anche conto della (8) il rapporto spire

è il rapporto tra la f.e.m. primaria e quella secondaria, ma anche il rapporto inverso delle correnti: come a dire che se il trasformatore eleva le tensioni nel passaggio dal primario al secondario, ne riduce le correnti nello stesso rapporto e ciò anche come conseguenza della conservazione della potenza.

Trascurando le c.d.t. primarie e secondarie (presenti le ultime con trasformatore a carico), il rapporto precedente diventa

Se anche la corrente a vuoto viene trascurata e si confonde la corrente di reazione I’₁ con quella totale I₁ assorbita dal primario può ritenersi ancora

Nello studio della macchina, quando è necessario procedere con maggiore rigore, si distinguono il rapporto spire

con il rapporto di trasformazione a vuoto K_o inteso, quest’ultimo, come rapporto fra la tensione nominale primaria U₁ e quella nominale secondaria U_2O che si ottiene nel funzionamento a vuoto:

Il valore del rapporto di trasformazione K_o risulta quindi lievemente superiore al rapporto spire n, e può facilmente essere misurato alimentando il trasformatore nel funzionamento a vuoto, a qualunque valore di tensione (il rapporto non cambia al variare della tensione di alimentazione).

-         Equazioni relative al secondario

Fig. 7)  Schema elettrico completo della macchina funzionante a carico.

Per la maglia del secondario si ottiene, considerando lo schema di fig. 7):

essendo

la tensione ai morsetti d’uscita del trasformatore e quindi la tensione al carico, che in seguito si preferirà chiamare U₂ .

Dallo schema relativo al secondario, nota l’impedenza del carico , in modulo e argomento,  si determina, per la legge di Ohm:

il cui modulo e sfasamento rispetto al vettore E₂ valgono rispettivamente

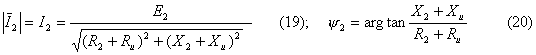
Per il primario, tenendo conto della corrente di reazione e della corrente totale I₁, per il secondo principio di Kirchhoff

 mentre per le correnti, per il 1° principio di Kirchhoff

Fig. 8) Diagramma vettoriale tensioni-correnti del trasformatore a carico

Le precedenti equazioni giustificano appieno il diagramma del trasformatore sotto carico (fig. 8) che viene costruito:

-         partendo dal flusso,

-         disponendo a 90° in ritardo le f.e.m. indotte primaria E₁ e secondaria E₂,

-         posizionando la corrente secondaria di modulo dato dalla (19) e sfasata di ψ₂ rispetto alla f.e.m. E₂ (relazione 20),

-         determinando vettorialmente, dalla (18), la tensione al carico

;

-         tracciando al primario la corrente di reazione che, ricordando la (16), ha modulo

      ed è in opposizione di fase rispetto alla I₂;

-         eseguendo la somma vettoriale

;

-         determinando la tensione di alimentazione sommando al vettore –E₁ le c.d.t. del primario, come indicato dall’equazione

.

Lo sfasamento φ_u  tra la tensione al carico U_u (che in seguito, come già detto, sarà chiamata U₂ , intesa come tensione secondaria a carico) e la corrente secondaria I₂ è naturalmente l’angolo caratteristico della impedenza del carico Z_u; lo sfasamento tra la tensione di alimentazione U₁ e la corrente totale primaria I₁ è l’angolo  con cui “viene visto” il trasformatore, comprensivo del carico, dal generatore di rete U₁, fornitore dell’energia.